GUÍA DE LOGARITMOS PROFESOR MARIO SAAVEDRA DÍAZ I
EJERCICIOS DE LOGARITMOS I ) CALCULAR 1 )EJERCICIOS DE LOGARITMOS I CALCULA EL VALOR DE X
GUÍA DE LOGARITMOS PROFESOR MARIO SAAVEDRA DÍAZ I
GUIÓN PARA EL TEMA DE LOGARITMOS 1 INTRODUCCIÓN PLANTEAR
LECCIÓN 2 POTENCIAS LOGARITMOS Y RAÍCES ENÉSIMAS OBJETIVO DE
TAREA 2POTENCIAS Y LOGARITMOSTELETONDOC TAREA 2POTENCIAS Y LOGARITMOSDOC
Guía de Logaritmos
Guía de Logaritmos
Profesor: Mario Saavedra Díaz
I Determine aplicando la definición.
a) log2x = 4 b) log5x = 0 c) log3/4x = 2 d) log1/2x = -3
e) loxx81 = 4 f) logx16 = -4 g) logx(1/8) = 3 h) log264 = x
i) log3(1/81) = x j) log4x = 3/2 k) logx4 = -2/5 l) log1/64x = 5/6
II Calcular el valor de:
a)
log3
81 + log4
64 – log2
128 b)
![]() c)
c)
![]()
d)
9log7
49 – 8log3
27 + 5log2
128 e)
![]() f)
f)
![]()
g)
![]() h)
h)
![]() i)
i)
![]()
III Desarrolla aplicando las propiedades de los logaritmos:
a) log 3ab b) log 5a/2 c) log 4a2/3 d) log a3b5
e)
log 2/ab f) log![]() g)
g)
![]()
![]() h)
h)
![]()
i)
![]() log j)
log j)
![]() k)
k)
![]() l)
log (abc)3
l)
log (abc)3
m)log (a2 - b2) n)log (a4 - b4) ñ) log [(m - n)/2]
IV Reduce las expresiones siguientes a un solo logaritmo:
a) log a + log b b) log x - log y c) 1/2 log x + 1/2 log y
d) log a - log b - log c e) log a + log b - log c - log d f) log x - 2 log y + log z
g) 2/5 log a + 3/5 log b h) log a + 1/2 log b - 4 log c i) 1/2 log a - 2/3 log b + 3/4 log c
j) log (x + y) - log 3 k) 1/3(log a - 3log b) + 1/4(log c - 3log d)
V Sabiendo que log 2 = 0,30; log 3 = 0,47; log 5 = 0,69 y log 7 = 0,84; calcula, sólo utilizando estos valores, los siguientes logaritmos:
a) log 30 b) log 12 c) log 81 d) log 42 e) log (4/9)
f) log (8/49) g) log (5/7) h) log 3,5 i) 2log 250 j) (log 18)· (log 16)
Tags: logaritmos ==================, profesor, mario, logaritmos, saavedra
- SUPERMARKTRECHERCHE DIESES ANGEBOT HAT DER MARKT BIERE SO
- BACKGROUNDER NEW KONICA MINOLTA SINGLE LENS REFLEX (SLR)TYPE DIGITAL
- J URIDISKĀM PERSONĀM SIA NESTE LATVIJA 1 (1)
- DEED IN REDEMPTION OF GROUND RENT THIS DEED MADE
- ANEXO I – CASOS DE USO PILOTO
- W ZÓR POZWU O EKSMISJĘ … … … …
- NAME DATE CHAPTER 3 PARALLEL AND PERPENDICULAR
- FUNERAL DEL PADRE SEBASTIÁN ALDOMÁ BONJOCH SANTIAGO DE CALI
- (LOGO DE LA COOPERATIVA) MANUAL DE CRÉDITO COOPERATIVA DE
- ANEXO III VALORACION DE TROFEOS PARA DETERMINAR SU CUOTA
- ANUARIO FEBRERO 2011 MARZO 2012 COMITÉ EMPRESA PERSONAL LABORAL
- MAISON CULTURELLE DE QUAREGNON TARIF D’OCCUPATION DE LA SALLE
- EVALUATION OF DEPARTMENT CHAIRPERSON COLLEGE OF SCIENCE AND ENGINEERING
- 4 ỦY BAN NHÂN DÂN CỘNG HÒA XÃ HỘI
- SECTION 0400 ‑ REIMBURSEMENT PROCEDURE 15A NCAC 02P 0401
- SYLLABUS SME 610 FUNDAMENTALS IN SERVICE MANAGEMENT IN THE
- VOTRE RUE DEVIENT TEMPORAIREMENT UNE OPENSTREETS RUE RÉSERVÉE
- C ONTENT CREATION POWERPOINT® INTERACTIVE TEXT BOXES POWERPOINT® INTERACTIVE
- POJEDINAČNI ZAHTJEV ZA VREDNOVANJE TRAJNOG USAVRŠAVANJA TRAJNO USAVRŠAVANJE U
- X366IE V005 PORK RAPID IMMUNOCHROMATOGRAPHIC TEST FOR QUALITATIVE DETERMINATION
- POWERPLUSWATERMARKOBJECT330883345 A KADEMIA SPECJALISTÓW FINANSUS PRZY FINANSUS AS SP
- JUMPING LESSON PLAN DATE 41105 TEACHER WESLEY COLEMAN SCHOOL
- 2 ธันวาคม 2555 เรื่อง ฝึกอบรมการใช้งานโปรแกรมใบขนสินค้าขาเข้าและขาออก SHIPPING EXPRESS (PAPERLESS) เรียน
- 25 WHAT IS SCIENCE? METHODOLOGICAL PITFALLS UNDERLYING THE EMPIRICAL
- TÜRKİYE BİNİCİLİK FEDERASYONU YARIŞMA PROGRAMI KONTROL LİSTESİ VE PROTOKOL
- DRAFT PROGRAMME (AS OF 30 JANUARY 2009) UNECEFAO TIMBER
- SHARIFUL HASAN SHAIKOT CELL 4058801213 EMAIL SHAIKOTWEBYAHOOCOM
- 4H EXHIBIT WRITEUP NAME GRADE AS OF LAST SEPTEMBER
- MATEMÁTICAS 1º ESO S I S T E M
- PRESUPUESTO AÑO 2020 MEMORIA DE CONFORMIDAD CON
REZULTATI PRVENSTVA SRBIJE U VIŠEBOJIMA U DVORANI BEOGRAD 06032016
 7 Statistično Raziskovanje Dejavnost Zasebnih Raziskovalcev 2015 Metodološko
7 Statistično Raziskovanje Dejavnost Zasebnih Raziskovalcev 2015 MetodološkoNZQA UNIT STANDARD 25563 VERSION 4 PAGE 3 OF
Southern Interior Mountains Ecoprovince Version 22 Written and Edited
 PROCEDURE FERRITIN OSR61203 THIS PROCEDURE IS VALID FOR THE
PROCEDURE FERRITIN OSR61203 THIS PROCEDURE IS VALID FOR THEORDINANCE NO 9673 (NS) AN ORDINANCE ADDING ARTICLE 22
INFORMAŢIILE DE INTERES PUBLIC PREZENTARE GENERALĂ ORICE PERSOANĂ POATE
MINNEAPOLIS MINNESOTA ENERGY PATHWAYS PROJECT TRANSCRIPT SPEAKERS BRIAN ROSS
 11 TRANSCRIVIU FONÈTICAMENT LES PARAULES O ELS SONS EN
11 TRANSCRIVIU FONÈTICAMENT LES PARAULES O ELS SONS ENMINISTERIO DE MEDIO AMBIENTE CONFEDERACIÓN HIDROGRÁFICA DEL GUADALQUIVIR PLAZA
Staffing Changes a Warm Welcome to all new Members
BIL 4588 TYP HOUSE RESOLUTION HR INB HOUSE IND
ORCAD® LAYOUT TO ALLEGRO® ALLEGRO PCB EDITOR TRANSLATOR PCB
 STRATEŠKI MANAGEMENT 1 3 DOMAČA NALOGA OBLIKOVANJE IN URESNIČEVANJE
STRATEŠKI MANAGEMENT 1 3 DOMAČA NALOGA OBLIKOVANJE IN URESNIČEVANJE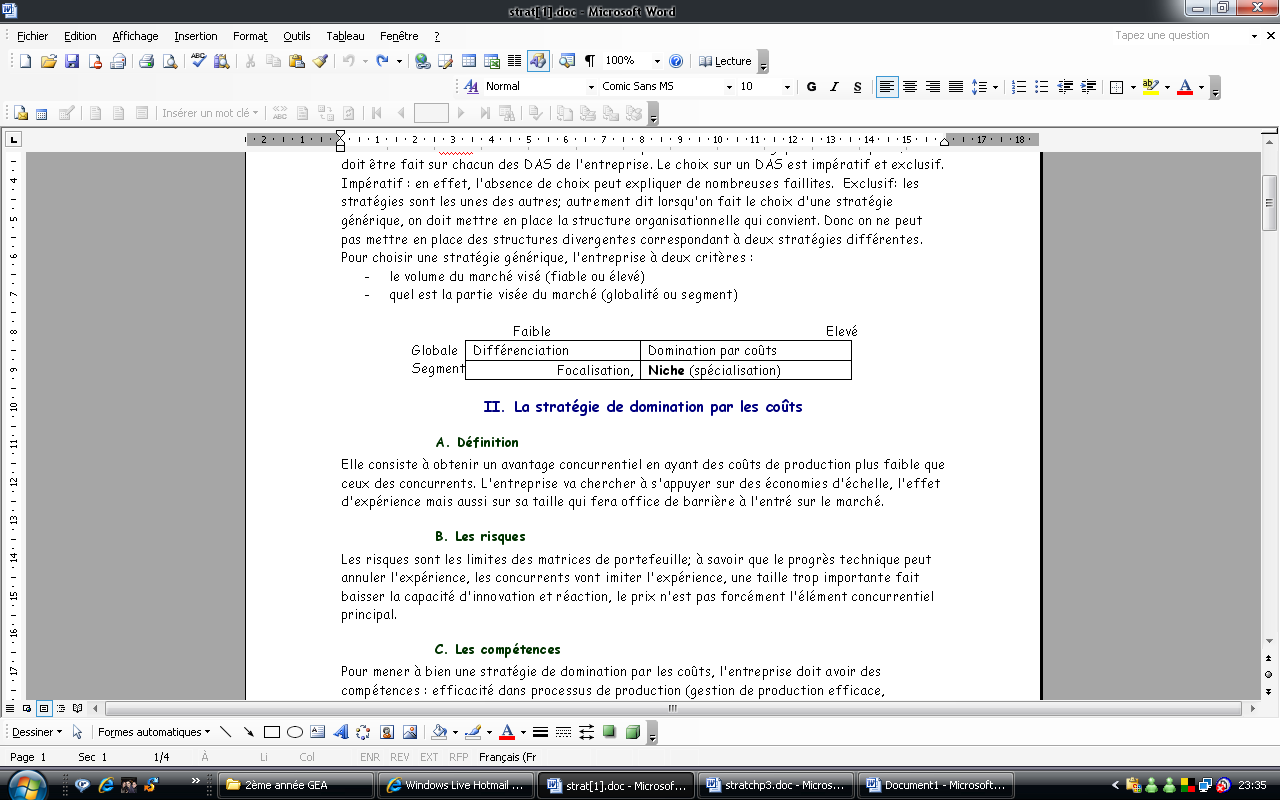 CHAPITRE 4 LES STRATÉGIES GÉNÉRIQUES ÉLÉMENTAIRES IDÉFINITION
CHAPITRE 4 LES STRATÉGIES GÉNÉRIQUES ÉLÉMENTAIRES IDÉFINITION SUSTAINABLE LOGGING PRACTICES REDUCED IMPACT LOGGING (RIL) PROVIDES ENVIRONMENTAL
 EDICIÓN Nº 52 DE 2004 BIOTECNOLOGÍA INDUSTRIAL ALIMENTARIA LA
EDICIÓN Nº 52 DE 2004 BIOTECNOLOGÍA INDUSTRIAL ALIMENTARIA LACURRICULUM VITAE JUAN CARLOS RODRÍGUEZ VÁSQUEZ NOMBRE JUAN CARLOS
 MINISTRY OF COMMUNITY SAFETY AND CORRECTIONAL SERVICES APPLICATION FOR
MINISTRY OF COMMUNITY SAFETY AND CORRECTIONAL SERVICES APPLICATION FORPOMYŚL O ŚRODOWISKU ZANIM WYDRUKUJESZ THINK ABOUT ENVIRONMENT BEFORE