TEMA 1 LOS NÚMEROS Y SUS PROPIEDADES 1 TIPOS

el Poder de la Generalización Números Mórficos Vamos a

---

---

TEMA 1: LOS NÚMEROS Y SUS PROPIEDADES

1. TIPOS DE NÚMEROS

Vamos a hacer un repaso por los diferentes tipos de números que nos podemos encontrar y cómo los representamos.

1. Los números naturales

El primer tipo de números del que tenemos que hablar son aquellos que nos permiten contar, estos son, los que nos permiten decir: dos manzanas, cinco libros, siete cartas, etc y se caracterizan por ser: positivos, sin decimales, sin fracciones…, es decir, naturales.

Los números naturales fueron los primeros que manejó el ser humano. Éstos se representan con el símbolo N y son:

{0, 1, 2, 3, 4, 5, 6, 7,..., 15, 16,..., 66, 67, 68,..., 12345, 12346,...}

En los números naturales siempre que se tenga un número existe su siguiente, que se obtiene del anterior sumándole uno.

La representación gráfica de los números naturales se hace sobre una semirrecta horizontal donde el extremo izquierdo es el 0. Desde aquí se divide la semirrecta en partes iguales, y en cada marca vamos situando los números ordenados de menor a mayor:

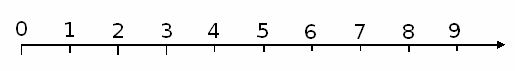
2. Los números enteros

La necesidad de tener números negativos es lo que nos lleva a definir los Números Enteros que no son ni más ni menos que los números naturales y estos mismos con signo negativo, es decir:

{...,−1234,−1233,...,−78,−77,...,−3,−2,−1,0,+1,+2,+3,...,+77,...,+1233,+1234,...}

A los números enteros se les identifica con el símbolo Z.

Como primera consecuencia de lo que hemos escrito anteriormente es que:

• Los números naturales son números enteros, pero no todos los números enteros son números naturales. Además la gran diferencia entre los números naturales y los números enteros es que los números enteros tienen opuesto, mientras que los números naturales no.

• Todo número entero tiene anterior y siguiente, esto es, dado un número entero siempre puedo escribir un número mayor y un número menor que él simplemente con sumarle o restarle uno.

• El opuesto de un número entero es el mismo número pero cambiado de signo.

EJEMPLOS:

1. El opuesto de -5 es +5.

2. El opuesto de +8 es -8.

Para representar los números enteros seguimos los siguientes pasos:

1. Trazamos una recta horizontal y situamos en ella el 0. El 0 divide a la recta en dos semirrectas.

2. Dividimos cada una de las dos semirrectas en partes iguales

3. Situamos los números enteros sobre las semirrectas: los enteros positivos a la derecha del cero, y los enteros negativos a la izquierda del cero.

Es decir, quedaría de la siguiente forma:

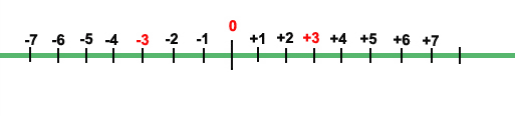
Antes de continuar definimos lo que se llama valor absoluto de un número, que se representa escribiendo el número dado entre dos barras verticales (I −7 I, se lee valor absoluto de -7). El valor absoluto de un número entero es el número natural que se obtiene al quitarle el signo al número inicial, luego −7=7. El valor absoluto de un número representa la distancia de ese número al origen de la recta numérica, es decir, al 0.

EJEMPLOS:

a) I+5I = 5

b) I−12I = 12

c) I14I = 14

d) I−8I = 8

A la hora de ordenar los números enteros se cumplen las siguientes reglas:

1. Cualquier número entero positivo es mayor que cualquier número entero negativo.

2. El cero es mayor que cualquier número entero negativo y menor que cualquier número entero positivo.

3. Dados dos números enteros positivos es mayor el que tiene mayor valor absoluto.

4. Dados dos números enteros negativos es mayor el que tiene menor valor absoluto.

3. Los números racionales

Los números racionales son aquellos que podemos expresar mediante una fracción de la forma a/b, donde a recibe el nombre de numerador, y b recibe el nombre de denominador. De esta forma, un número racional es una fracción donde:

1. a y b son números enteros.

2. b no puede ser 0.

A todos los números racionales se les designa con el símbolo Q.

Algunas consecuencias de la definición de número racional son:

1. Todo número natural es racional. Ejemplo: 2 = 4/2

2. Todo número entero es racional. Ejemplo: -3 = -6/2

3. Como recordarás, el inverso de un número es aquel que al multiplicarlo por el número da como resultado 1, es decir, dado un número racional a/b, su inverso es b/a ya que (a/b)·(b/a) = (a·b)/(b·a) = 1

Todos los números racionales, salvo el cero, tienen inverso. Esta es la característica más importante que diferencian a los racionales de los enteros, ya que en los números enteros, solamente el 1 tiene inverso que es el mismo.

Por lo tanto, dado un número racional a/b, su inverso es b/a.

Para representar los números racionales hay que seguir los siguientes pasos:

1. Dibujamos la recta numérica:

2. Dividimos cada segmento unidad en b partes iguales.

3. Contamos a partes, de en las que hemos dividido ahora la recta, desde el 0 y en el sentido de su signo.

4. Luego representamos el número:

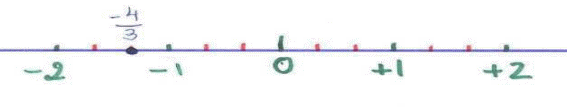
4. Los números irracionales

Ya hemos visto los números naturales, enteros y racionales, pero aún queda un tipo de números, estos son los números irracionales, que son aquellos números que tienen infinitas cifras decimales no periódicas. Algunos de estos números son: π,φ, √2, √3,...

Para saber si un número irracional es mayor o menor que otro se hace de forma aproximada, se calcula el número en la calculadora, se representa aproximadamente en la recta numérica y el que se quede más a la izquierda es el menor.

5. Los números reales

A lo largo de este tema hemos estudiado los números naturales, enteros, racionales e irracionales. A todos estos números juntos se les llama números reales.

Los números reales se representan sobre la recta numérica que toma el nombre de los números que contiene y se denomina recta real. A cada punto de la recta le corresponde un número real y a cada número real un punto de la recta.

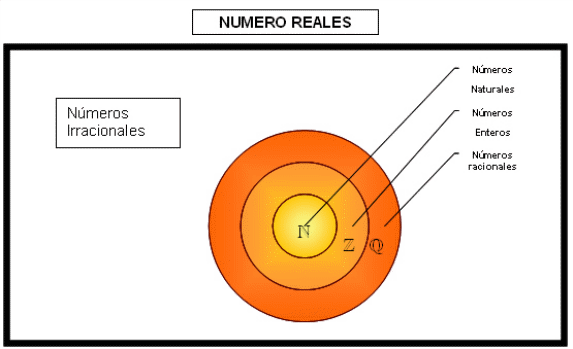
• Intervalos

Se llama intervalo determinado por dos números reales, a todos los números que se pueden representar en la recta real entre ambos, es decir, a todos los números que puedo colocar en el segmento de recta real determinado por esos dos números reales.

EJEMPLO:

El intervalo entre -1 y 2 es, gráficamente, la zona coloreada de rojo en la recta real:

A los números que determinan el intervalo se les denomina extremos y dependiendo de si los extremos se incluyen en el intervalo o no la forma de escribirlo matemáticamente varía. Cuando los extremos pertenecen al intervalo se usan los símbolos [0 ] y si los extremos no están dentro del intervalos se usan los símbolos (0). Los extremos, a la hora de escribir, se ponen de menor a mayor.

Una propiedad importante de los intervalos es que están formados por infinitos números reales.

Veamos algunos ejemplos para ilustrar lo anterior:

1. Intervalo [−1, 2], es el que tenemos representado en el dibujo anterior. En este caso hemos considerado que tanto el -1 como el 2 están dentro del intervalo.

6. Máximo común divisor de un conjunto de números

El máximo común divisor de un conjunto de números se define como el divisor común mayor.

Este es un concepto que vas a comprender muy bien con el siguiente ejemplo:

Los divisores del 24 son: 24, 12, 8, 6, 4, 3, 2 y 1

Los divisores del 90 son: 90, 45, 30, 18, 15, 10, 9, 6, 5, 3, 2 y 1

Los números señalados en negrita son divisores comunes a 24 y 90 y el mayor de todos esos divisores es el 6. Luego el 6 es el máximo común divisor.

Método general para calcular el M.C.D. de un conjunto de números

Calculemos el máximo común divisor de 12 y de 30:

1º. Descomponemos los números en producto de factores primos:

12=2² ·3

30= 2·3·5

2º. El máximo común divisor es el producto de los factores comunes con el menor exponente:

M.C.D. (12,30)= 2 · 3 = 6

7. Mínimo común múltiplo de un conjunto de números

El mínimo común múltiplo de un conjunto de números es el múltiplo común más pequeño.

Este es un concepto que vas a comprender muy bien con el siguiente ejemplo:

Los múltiplos del 6 son: 6; 12; 18; 24; 30; 36; 42; 48;...

Los múltiplos del 4 son: 4, 8; 12; 16; 20; 24; 28; 32; 36;…

Los números marcados en negrita son múltiplos comunes a ambos y el mínimo común múltiplo (m.c.m.) es el más pequeño de los comunes; es decir el 12.

Método general para calcular el m.c.m. de un conjunto de números

Calculemos el m.c.m. de 12 y de 30:

1º. Descomponemos los números en producto de factores primos:

12=2² ·3

30= 2·3·5

2º. El mínimo común múltiplo es el producto de los factores comunes, eligiendo el que tiene mayor exponente, y los factores no comunes:

m.c.m. (12,30) = 22 · 3 · 5 = 4 · 3 · 5 = 60

2. POTENCIAS

Se denomina potencia de un número al resultado que obtenemos de la sucesiva multiplicación de un número por sí mismo. Así, una potencia es un modo abreviado de escribir un producto de un número por sí mismo.

En la expresión de la potencia de un número consideramos dos partes:

• La base es el número que se multiplica por sí mismo.

• El exponente es el número que indica las veces que la base aparece como factor.

Exponente 3 porque el 5 aparece 3 veces como factor

5³ = 5·5·5 = 125

Base 5: es el número que se multiplica por sí mismo

2.1 Operaciones con potencias

• Cualquier número elevado al exponente 1 es igual al mismo número.

a¹ = a; 3¹ = 3

• Cualquier número elevado al exponente 0 es igual a 1.

a⁰ = 1; 3⁰ = 1

1. Producto de potencias de la misma base

Para multiplicar potencias de la misma base se deja la misma base y se suman los exponentes:

a^m · aⁿ = a^m+n

2. Cociente de potencias de la misma base

Para dividir potencias de la misma base se deja la misma base y se restan los exponentes:

a^m : aⁿ = a^m-n

3. Potencia de exponente negativo

Una potencia de exponente negativo equivale al inverso de esa potencia con exponente positivo. Es decir:

a^-b = 1/a^b

4. Potencias de base negativa

Al elevar un número negativo a un exponente par el resultado es siempre positivo. En cambio, si lo elevamos a un exponente impar, el resultado es siempre negativo. Por ejemplo:

(-5)⁴ = (-5) · (-5) · (-5) · (-5) = 625 El resultado es positivo

(-5)³ = (-5) · (-5) · (-5) = -125 El resultado es negativo

5. Potencia de otra potencia

Para elevar una potencia a otra potencia, se deja la misma base y se multiplican los exponentes:

(a^m)ⁿ = a^m·n

6. Potencia de un producto

La potencia de un producto equivale al producto de potencias cuyas bases son cada uno de los factores y cuyo exponente es el mismo:

(a · b)^m = a^m · b^m

2. La notación científica

Escribir un número en notación científica es expresarlo como el producto de un número (entero o decimal entre 1 y 10), y una potencia de base 10.

Ejemplos:

a) 529000000 = 5,29 · 10⁸ b) 590000000000 = 5,9 · 10¹¹

c) 0,000987 = 9,87 · 10^-4 d) 0,000000045 = 4,5 · 10^-8

Como puedes ver las "potencias de 10" son una manera muy útil de escribir números muy grandes o muy pequeños, ya que en lugar de poner muchos ceros, puedes poner qué potencia de 10 necesitas para hacer todos esos ceros, porque como sabemos:

Toda potencia de base 10 es igual a la unidad seguida de tantos ceros como unidades tiene el exponente.

Ejemplos:

10² = 100; 10³ = 1000; 10⁴= 10000

• Para expresar números muy grandes en notación científica, basta con:

1. Escribir las cifras significativas, colocando una coma a la derecha de la primera.

2. Contar las cifras que hay a la derecha de la coma, lo que nos dará el exponente al que hay que elevar el 10.

• Para expresar en notación científica números muy pequeños, actuamos de forma parecida, sólo que en este caso el exponente del 10 será negativo.

1. Escribir las cifras significativas, colocando una coma a la derecha de la primera.

2. Contar el lugar que ocupa la primera cifra significativa a partir de la coma. Esto nos dará el valor absoluto del exponente (negativo).

Ejemplos:

• Número muy grande: 95000000000000000000 = 9,5 · 10¹⁹

• Número muy pequeño: 0,000987 = 9,87 ⋅10^-4

• Operaciones con números expresados en notación científica.

La notación científica también es útil para realizar operaciones con números muy grandes o muy pequeños de forma fácil y cómoda. Así, llamamos orden de magnitud de un número al exponente al que está elevado el 10 cuando el número está escrito en notación científica.

A. Suma y resta:

a. Las potencias de 10 son iguales:

En este caso, sumamos o restamos los números que preceden a las potencias de 10, dejando el 10 elevado al mismo exponente.

Ejemplos: 2 · 10^-3 + 4,9 · 10^-3 = (2 + 4,9) · 10^-3= 6,9 · 10^-3

-5 · 10⁶ + 7 · 10⁶ = (-5 + 7) · 10⁶ = 2 · 10⁶

b. Las potencias de 10 son distintas:

Si son distintas no podemos sumar ni restar directamente, sino que antes tenemos que conseguir que sean iguales. Actuaremos de la siguiente forma:

Supongamos que tenemos que realizar la siguiente operación:

4,2 · 10⁴ - 3,1 · 10³

1) Reducimos a la potencia de 10 de menor exponente (para ello podemos descomponer en producto la potencia de exponente mayor).

4,2 · 10¹ · 10³ - 3,1 · 10³ = 42 · 10³ - 3,1 · 10³

2) Sumamos o restamos los números que van delante de las potencias de base 10:

(42 - 3,1) · 10³ = 38,9 · 10³

3) Finalmente, escribimos el resultado correctamente en notación científica:

38,9 · 10³ = 3,89 · 10⁴

Si los exponentes fueran negativos, el procedimiento es el mismo. Veamos el siguiente ejemplo: -6,1 · 10^-3 - 7 · 10^-2

1) -6,1 · 10^-3 - 7 · 10¹ · 10^-3 = -6,1 · 10^-3 - 70 · 10^-3

2) (-6,1 - 70) · 10^-3 = -76,1 · 10^-3

3) -76,1 · 10^-3 = -7,61 · 10^-2

B. Multiplicación

Para multiplicar dos números en notación científica, se multiplican los números que preceden a las potencias de 10 y se multiplican también dichas potencias (que al ser potencias de la misma base, se suman los exponentes).

Ejemplos: (4 · 10⁵) · (2 · 10⁷) = (4 · 2) · (10⁵ · 10⁷) = 8 · 10¹²

(-2 · 10^-4) · (7 · 10^-11) = (-2 · 7) · (10^-4 · 10^-11) = -14 · 10^-15=-1,4 · 10^-14

C. División

Para dividir dos números en notación científica, se dividen los números que preceden a las potencias de 10 y también dichas potencias (que al ser potencias de la misma base, se restan los exponentes).

Ejemplos:

(4,7 · 10²) : (9,4 · 10⁶) = (4,7 : 9,4) · (10² : 10⁶) = 0,5 · 10^-4 = 5 · 10^-5

(-1,8 · 10^-11) : (-3 · 10^-16) = (1,8 : 3) · (10^-11 : 10^-16) = 0,6 · 10⁵ = 6 ·10⁴

2. RADICALES

Se llama raíz n-ésima de un número a, y se escribe , a un número b que elevado a n nos dé a, de manera que se llama radical; a es el radicando; y n índice de la raíz.

Ejemplos:

1. FORMA EXPONENCIAL DE LOS RADICALES

La raíz n-ésima de un número puede expresarse también en forma de potencia:

Esta nomenclatura es coherente con la definición, ya que:

Es importante familiarizarse con la forma exponencial de los radicales, pues nos permitirá expresarlos y operar con ellos usando las propiedades de las potencias.

Ejemplos:

2. EXISTENCIA DE RADICALES

Primera: si a es positivo, existe, cualquiera que sea el valor de n.

Segunda: si a es negativo, sólo existen sus raíces si n es de índice impar.

Tercera: salvo que a sea una potencia n-ésima de un número entero o fraccionario, es un número irracional, por lo que sólo podremos obtener su expresión decimal aproximada.

3. PROPIEDADES DE LOS RADICALES

Los radicales tienen una serie de propiedades, que son consecuencia inmediata de las propiedades de las potencias.

Primera: Esta propiedad nos permite simplificar radicales y para conseguir que dos o más radicales tengan el mismo índice (reducir a índice común).

Ejemplo:

Segunda: Esta propiedad nos permite sacar un factor fuera de la raíz o de modo contrario, juntar varios radicales en uno sólo:

Ejemplos:

Tercera: Esta propiedad, junto con la primera y segunda, sirve para poner productos y cocientes de radicales bajo una sola raíz.

Ejemplo:

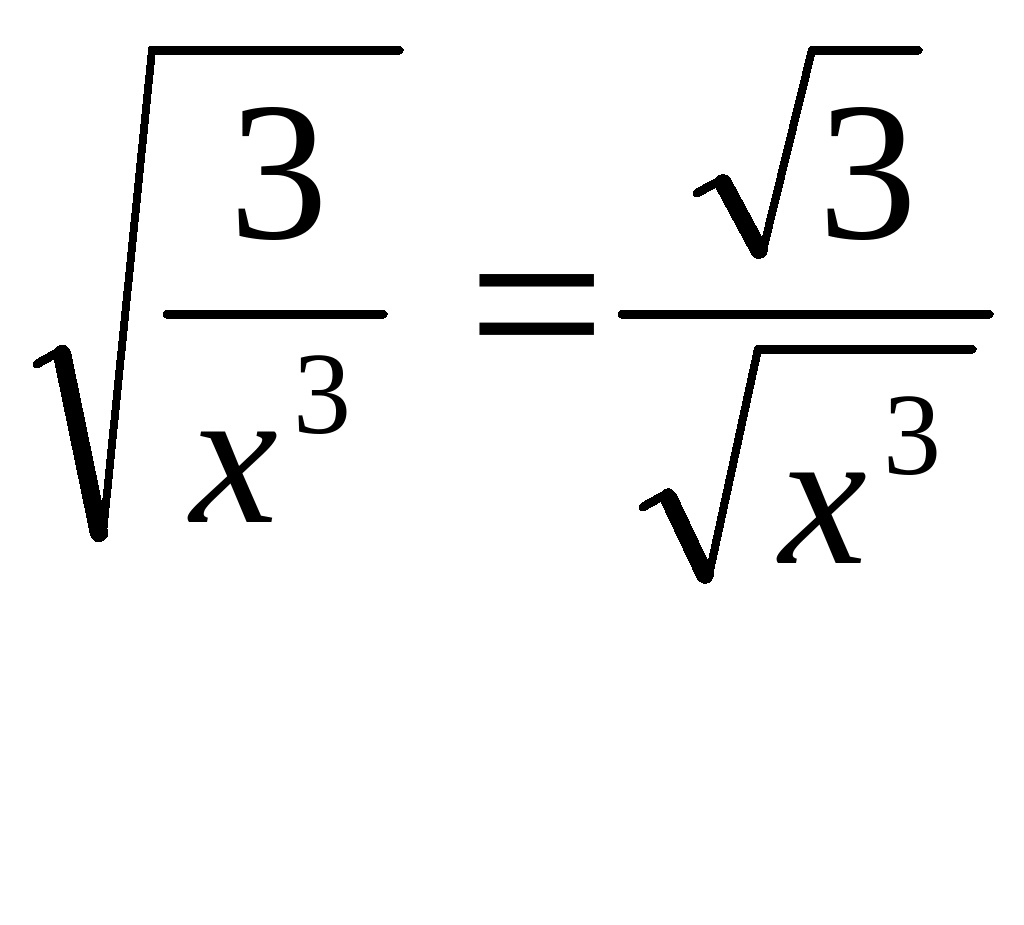
Cuarta: Esta propiedad nos permite simplificar expresiones con raíces.

Ejemplos:

Quinta: Esta propiedad nos permite simplificar expresiones con raíces.

4. RADICALES SEMEJANTES

Dos radicales son semejantes cuando tienen el mismo índice y el mismo radicando, de manera que los radicales y son semejantes ya que tienen el mismo índice, 2, y el mismo radicando, 3.

Más ejemplos de radicales semejantes:

OPERACIONES CON RADICALES

1. SUMA Y RESTA

La suma o la resta de radicales semejantes es otro radical semejante a los dados, cuyo coeficiente es igual a la suma o la resta de los coeficientes de los radicales sumados o restados.

Ejemplo:

Si los radicales no son semejantes, la suma se deja indicada.

Ejemplo:

2. PRODUCTO

El producto de radicales, con el mismo índice, es igual a otro radical cuyo coeficiente y radicando son iguales, respectivamente, a los productos de los coeficientes y radicandos de los factores.

Ejemplo:

3. COCIENTE

El cociente de dos radicales con el mismo índice, es igual a otro radical, cuyo coeficiente y radicando son iguales, respectivamente, al cociente de los coeficientes y radicandos de los radicales dividendo y divisor.

Ejemplo:

4. POTENCIA

La potencia de un radical es igual a otro radical, cuyo coeficiente y radicando están elevados a dicha potencia.

Ejemplo:

Es importante observar que al elevar al cuadrado un radical de índice 2, se obtiene el radicando.

Ejemplo:

5. Racionalización de radicales

Se debe evitar que una raíz quede en el denominador ya que complica la comparación con otra expresión o estimar su valor. Para ello hay que multiplicar el numerador y el denominador por la misma raíz de la siguiente forma:

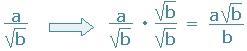
En esta expresión tenemos dos términos en el denominador, el cual se puede racionalizar multiplicando por ya que formarán una Suma por Diferencia, lo que permite eliminar las raíces en el denominador.

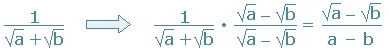
3. LOGARITMOS

Se llama Logaritmo en base a de x, al exponente al que hay que elevar la base a para obtener x:

De la definición de logaritmo podemos deducir las siguientes propiedades:

1. No existe el logaritmo de un número con base negativa.

2. No existe el logaritmo de un número negativo.

3. No existe el logaritmo de cero.

4. El logaritmo de 1 es cero.

5. El logaritmo en base a de a es uno.

6. El logaritmo en base a de una potencia en base a es igual al exponente.

7. El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

8. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.

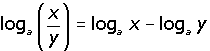
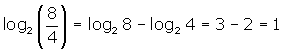
9. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.

10. El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.

11. Cambio de base:

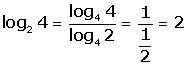
Tags: números y, los números, números, propiedades, tipos

---

• VULNERABILITY AND CAPACITY ASSESSMENT KEY ELEMENTS OF A SUCCESS
• TITLUL LUCRĂRII (TIMES NEW ROMAN 14 PT BOLD CAPS)1
• C RÓNICA FESTIVAL BLUES LEGANES (MADRID) 9 A 12
• SOLICITUD DE PAGO DE LIBRANZA JUDICIAL Y TRANSFERENCIA DE
• [COMUNICAZIONE DI AVVENUTO UTILIZZO] (SU CARTA INTESTATA DELL’IMPRESA RICHIEDENTE)
• ¿HUBO UNA PRÁCTICA RETÓRICA EN LA ANTIGUA CHINA? ALGUNOS
• CONSEJERÍA DE MEDIO AMBIENTE Y ORDENACIÓN TERRITORIAL VICECONSEJERÍA DE
• !DOCTYPE HTML HTML LANGENUS HEAD META CHARSETUTF8 META NAMEVIEWPORT
• A 2 KALIUMPERMANGANAT KALIUMPERMANGANAT FINDET ALS STARKES OXIDATIONSMITTEL SOWOHL
• ELOSZO FOTOZAS ES KIRANDULAS SZEMPONTJABOL IGEN GAZDAG EVET ZARTUNK
• PAVYZDINĖ FORMA (VARDAS PAVARDĖ) (ATSTOVO VARDAS IR
• PLIEGO DE CLÁUSULAS ADMINISTRATIVAS PARTICULARES PARA LA ADJUDICACIÓN POR
• KONTOPLAN FOR LØRENSKOG KOMMUNE GJELDENDE FRA 2016 INNHOLD
• HTTPSERGIODELUZWORDPRESSCOM OFICINAS DE IBERCAJA ANDALUCÍA ALMERÍA RB OBISPO
• [HOSTELDAY CENTRE] ADDRESS ADDRESS ADDRESS POST CODE [DATE] TELEMAIL
• LA IMPORTANCIA DE LOS DERECHOS INTELECTUALES EN LA ECONOMÍA
• PUBLISHER PROGRAM TITLE COMPONENTS PUBLISHER PROGRAM TITLE COMPONENTS CALIFORNIA
• STANOVY KLUBU RARÁŠKŮ BÍLOVICELUTOTÍN I ÚVODNÍ USTANOVENÍ NÁZEV SÍDLO
• APRIL BREAKFAST DEXTER SCHOOL ◄ MARCH ~ APRIL 2019
• UNIVERSIDAD DE SALAMANCA SERVICIO GENERAL DE PREPARACIÓN DE ROCAS
• 6 C ENTRO DE CIENCIA BÁSICA UPB LABORATORIO FUNDAMENTOS
• 1 890 KJ IS RELEASED WHEN 1 MOLE OF
• PO ZAHODU ZDA IN HAVAJIH PRVO LETOŠNJE STROKOVNO IN
• LATE STAGE REVIEW (LSR) FORM BETWEEN 18 AND 24
• PAGE 3 OF 3 POLICY RAD2065 GUIDELINES RECOMMENDATIONS
• RUNNING RECORDS CONVENTIONS ACCURATE READING    
• 18 RECTÁNGULO COORDINADOR MINISTERIO DE MEDIO AMBIENTE
• STRUCTURA PROIECTULUI DE MANAGEMENT ELEMENTELE CARE TREBUIE ABORDATE A
• INFORMACJA PRASOWA REKORDOWE WYNIKI ID LOGISTICS OPERATOR PODSUMOWUJE
• CONVOCATORIA REFERENCIA 152017 TRABAJADORA SOCIAL PROGRAMA DE ACOGIDA

• VENTILATION GRILLE AL SPECIFICATION TEXTS ROOM AIRCONDITIONING MODULE READY
• NW INDEPENDENT LIVING MATTERS NEWSLETTER OF INDEPENDENT LIVING RESOURCES
• AV UNIVERSIDAD VERACRUZANA KM 8 COL STA CECILIA CP
• P ROGRESS RAG REPORT PROJECT ID [PROJECT ID]
• ARMY NATIONAL GUARD TRANSFORMATION AND IT’S CHANGING ROLE IN
• DOLNO20145083 UCHWAŁA NR LXVII43614 RADY MIEJSKIEJ W GŁOGOWIE Z
• FORMULARIO DE REMEDIACIÓN A6 HOJA 5 DE 5 SUBSECRETARIA
• VOLUNTEER ROLE OUTLINE IT VOLUNTEER BECOMING AN IT VOLUNTEER
• COLEGIO DE ARQUITECTOS DE SAN JUAN LEY 6026 REQUISITOS
• SOME PLOTS FROM ASTRONOMY I HUBBLE’S DATA BELOW YOU
• STŘEDNÍ PRŮMYSLOVÁ ŠKOLA KARVINÁ LABORATORNÍ PRÁCE Z FYZIKY II
• MODELO Y CONTENIDO ESENCIAL DE PERMISO Y AUTORIZACIÓN DE
• RECONSTITUER ET COMPRENDRE LES VARIATIONS CLIMATIQUES PASSÉES INTRODUCTION DIFFÉRENCE
• LINCOLN HIGH SCHOOL PORTFOLIO REQUIREMENTS & EXPECTATIONS FOR STUDENT
• ATENCIÓN PSICOLÓGICA EN HOSPITAL DESARROLLO INFANTIL Y NUTRICIÓN TALLERES
• ERDÉLYI MAGYAR MŰSZAKI TUDOMÁNYOS TÁRSASÁG TERMINOLÓGIA ERDÉLYI MAGYAR MŰSZAKI
• PLAN DE PUESTA EN PRÁCTICA DE STEPS RESUMEN INTRODUCCIÓN
• PROYECTO ROBOT AUTÓNOMO MÓVIL GIA – FRBA UTN PROTOCOLOS
• ODDELEK ZA KMETIJSKO SVETOVANJE TRNOVELJSKA CESTA 1
• VI CELE I WSKAŹNIKI PROCES TWORZENIA LOKALNEJ STRATEGII ROZWOJU