LIMITS OF FUNCTIONS USING THE SQUEEZE PRINCIPLE THE FOLLOWING

13 UNDERSTANDING OF LIMITS AND DIFFERENTIATION AS THRESHOLD CONCEPTS
14 ASYMMETRIC CONSTRAINTS ON LIMITS TO SPECIES RANGES INFLUENCE
2 FY 1999 HUD INCOME LIMITS BRIEFING MATERIAL US

---

2005 UNIT TOTAL DEVELOPMENT COST (TDC) LIMITS NUMBER OF
30 APRIL 2004 MEDIA STATEMENT HEAVY VEHICLE SPEED LIMITS
73506DOC DETECTING ENTREPRENEURSHIP HOW AND WITHIN WHAT LIMITS? CAN

---

LIMITS OF FUNCTIONS USING THE SQUEEZE PRINCIPLE

LIMITS OF FUNCTIONS USING THE SQUEEZE PRINCIPLE

The following problems involve the algebraic computation of limits using the Squeeze Principle, which is given below.

SQUEEZE PRINCIPLE : Assume that functions f , g , and h satisfy

and

.

Then

.

(NOTE : The quantity A may be a finite number, , or . The quantitiy L may be a finite number, , or .)

The Squeeze Principle is used on limit problems where the usual algebraic methods (factoring, conjugation, algebraic manipulation, etc.) are not effective. However, it requires that you be able to ``squeeze'' your problem in between two other ``simpler'' functions whose limits are easily computable and equal. The use of the Squeeze Principle requires accurate analysis, deft algebra skills, and careful use of inequalities.

SOLUTIONS TO LIMITS USING THE SQUEEZE PRINCIPLE

SOLUTION 1 : First note that

because of the well-known properties of the sine function. Since we are computing the limit as x goes to infinity, it is reasonable to assume that x > 0 . Thus,

.

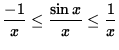Since

,

it follows from the Squeeze Principle that

.

SOLUTION 2 : First note that

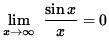because of the well-known properties of the cosine function. Now multiply by -1, reversing the inequalities and getting

or

.

Next, add 2 to each component to get

.

Since we are computing the limit as x goes to infinity, it is reasonable to assume that x + 3 > 0. Thus,

.

Since

,

it follows from the Squeeze Principle that

.

SOLUTION 3 : First note that

because of the well-known properties of the cosine function, and therefore

.

Since we are computing the limit as x goes to infinity, it is reasonable to assume that 3 - 2x < 0. Now divide each component by 3 - 2x, reversing the inequalities and getting

,

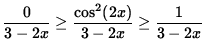or

.

Since

,

it follows from the Squeeze Principle that

.

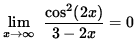SOLUTION 4 : Note that DOES NOT EXIST since values of oscillate between -1 and +1 as x approaches 0 from the left. However, this does NOT necessarily mean that does not exist ! ? #. Indeed, x³ < 0 and

for x < 0. Multiply each component by x³, reversing the inequalities and getting

or

.

Since

,

it follows from the Squeeze Principle that

.

SOLUTION 5 : First note that

,

so that

and

.

Since we are computing the limit as x goes to infinity, it is reasonable to assume that x+100 > 0. Thus, dividing by x+100 and multiplying by x², we get

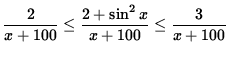
and

.

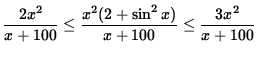Then

=

=

=

= .

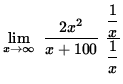
Similarly,

= .

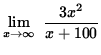Thus, it follows from the Squeeze Principle that

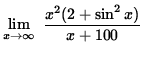= (does not exist).

SOLUTION 6 : First note that

,

so that

,

,

and

.

Then

=

=

=

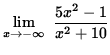
= 5 .

Similarly,

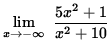= 5 .

Thus, it follows from the Squeeze Principle that

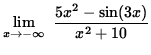= 5 .

SOLUTION 7 : First note that

and

,

so that

and

.

Since we are computing the limit as x goes to negative infinity, it is reasonable to assume that x-3 < 0. Thus, dividing by x-3, we get

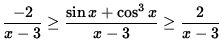
or

.

Now divide by x² + 1 and multiply by x² , getting

.

Then

=

=

=

=

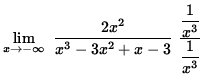
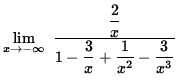
= 0 .

Similarly,

= 0 .

It follows from the Squeeze Principle that

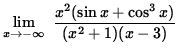= 0 .

SOLUTION 8 : Since

=

and

= ,

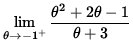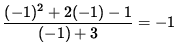it follows from the Squeeze Principle that

,

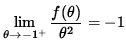that is,

.

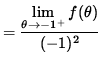
Thus,

.

SOLUTION 9 : a.) First note that (See diagram below.)

area of triangle OAD < area of sector OAC < area of triangle OBC .

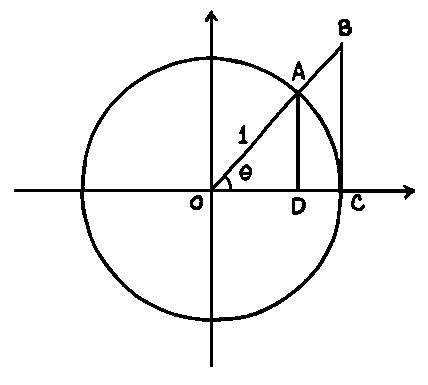
The area of triangle OAD is

(base) (height) .

The area of sector OAC is

(area of circle) .

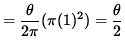The area of triangle OBC is

(base) (height) .

It follows that

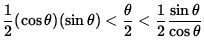
or

.

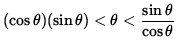b.) If , then and , so that dividing by results in

.

Taking reciprocals of these positive quantities gives

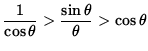
or

.

Since

,

it follows from the Squeeze Principle that

.

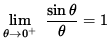SOLUTION 10 : Recall that function f is continuous at x=0 if

i.) f(0) is defined ,

ii.) exists ,

and

iii.) .

First note that it is given that

i.) f(0) = 0 .

Use the Squeeze Principle to compute . For we know that

,

so that

.

Since

it follows from the Squeeze Principle that

ii.) .

Finally,

iii.) ,

confirming that function f is continuous at x=0 .

A GE LIMITS FOR THE YOUNGER UMPIRES AS YOU
ADDITIONAL INSTRUCTIONS DISTRICT COUNTY ROUTE PM (KP) LIMITS EA
APPENDIX A UNSECURED CREDIT AND UNSECURED CREDIT LIMITS SUPPLEMENTAL

Tags: following problems, following, principle, squeeze, functions, limits, using

---

• HINTS FOR TEACHERS IN CHARGE OF SCHOOL ENTRIES SCHOOL
• INFORMATION ABOUT USING THE UTM PORTAL WHEN A STUDENT
• Building Management (third Party Risks Insurance) Regulation the
• SAMPLE BUDGET PAGE – ORGANIZATIONAL EVENT FINANCIAL INFORMATION
• KULTURÁLIS PÁLYÁZATOK ELBÍRÁLÁSA 2013 SSZ PÁLYÁZÓ MEGNEVEZÉS A PÁLYÁZAT
• PRILOGA 2 KOMBINACIJE UKREPA KOPOP A MOŽNE KOMBINACIJE UKREPA
• BIOLOGÍA 2º BACHILLER TEMA 3 LÍPIDOS 1 LÍPIDOS 1
• FUNCIONES ESTÁNDAR DE MSACCESS HERE IS A LIST OF
• A809 2 FISCAL NOTE ASSEMBLY NO 809 STATE OF
• Documentary Paper Clips Study Guide Book & Distance Learning
• PLEASE COMPLETE SIGN AND RETURN TO JIM DOW FOR
• B IENVENIDOS A SUS CANCHAS DE JUEGO
• D R CLIENT SATISFACTION PROCEDURES 20082009 REVISED 8142008
• FOR IMMEDIATE RELEASE JULY 17 2019 GOVERNOR WOLF ANNOUNCES
• KESİRLER ETKİNLİĞİ AŞAĞIDA VERILEN ŞEKILLERIN BÜTÜNÜ BOYAYINIZ 5NOKTA YILDIZ
• PAGE 0 MISSOURI GAMING COMMISSION RIVERBOAT GAMING APPLICATION YOU
• RESPONSABILIDADE GRUPO ESPÍRITA SEARA DO MESTRE WWWSEARADOMESTRECOMBREVANGELIZACAO VERÔNICA NÃO
• [ 2] COMMUNIQUÉ DE PRESSE RÉFÉRENCE STIEBEL ELTRON DATE
• C OMPRENSIÓN ESCRITA “POR UNA CIUDAD MÁS LIMPIA” ELIGE
• IRRIGATION & ELECTRICAL DISTRICTS ASSOCIATION OF ARIZONA RD
• ĽUDOVÁ SLOVESNOSŤ KUBOV ZAJAC (ĽUDOVÁ ROZPRÁVKA) KUBO ŠIEL POĽOM
• DIRECCION GENERAL DEL ARCHIVO NACIONAL DEPARTAMENTO SERVICIOS ARCHIVISTICOS EXTERNOS
• FAMILY SUPPORT SERVICE HMP & YOI READING 36 FORBURY
• 0214 GROUNDWATER TEMPERATURE (EDITION 2011) OVERVIEW THE
• OD LETA 1894 VINARSKA ULICA 14 2000 MARIBOR TEL
• SAMPLE OFFER LETTER HOURLY ADMINISTRATIVE PROFESSIONAL NONCONTINUOUS DEAR [APPLICANT’S
• RETI DI CITTÀ – CITTÀ DI PALERMO SCHEDA B
• AMERICAN FOOD A GLOBAL HISTORY WE’LL HAVE WHAT THEY’RE
• W ZGODZIE Z TERMINAMI CZYLI KIEDY ZACZYNAMY I KIEDY
• ALLERDALE BOROUGH COUNCIL CARAVAN SITES AND CONTROL OF DEVELOPMENT

• EXPERIMENT 543F[2] – PREPARATION OF METHYL 3NITROBENZOATE IN TWO
• CATALOGO VISUAL DE FONEMAS PARA EL APRENDIZAJE Y REFUERZO
• RENCANA PELAKSANAAN PEMBELAJARAN (RPP) NAMA SEKOLAH SMA MA’ARIF
• SOCIAL INEQUALITY RACEETHNICITY GENDER AND CLASS & STRATIFICATION DEPARTMENT
• TRUST PRODUCTION OFFICE APPLICATIONREGISTRATION AS PERMITTED BY SECTION 71590
• DOMANDA PER L’ATTIVAZIONE DEL SERVIZIO DI ASSISTENZA EDUCATIVA SCOLASTICA
• REVIEW OF WINTER PRECIPITATION GUIDELINES 1000500 MB THICKNESS
• JUNTOS NADA MÁS AUTORA ANNA GAVALDA C AMILLE FAUQUE
• PRŮMĚRNÝ VĚK KANDIDÁTEK JEDNOTLIVÝCH STRAN – MOST DĚLNICKÁ STRANA
• ZAŁĄCZNIK NR 2 UMOWA ZLECENIA NR (UMOWA PODLEGA
• PÚBLICO FTAATNCCBFINF29 3 DE OCTUBRE DE 2000 ORIGINAL ESPAÑOL
• CONFIDENCIALIDAD ANULADA FTAASMEINF95 12 DE AGOSTO DE 2003 ORIGINAL
• Ðïࡱáþÿ ¥á9 пx96gbjbjýïýï Rx9f¥x9f¥x96cÿÿÿÿÿÿljjjjjjj~èèèè Ô~çüüüüüüüüfhhhhhhß Ÿ^ljüüüüül´ Jjüüx81´ ´
• ZAŁĄCZNIK DO ZARZĄDZENIA NR 462014 REGULAMIN SIECI KOMPUTEROWEJ UNIWERSYTETU
• REGULAMIN SZKOLEÑ CENTRUM EDUKACYJNOSZKOLENIOWEGO 1 PODSTAWOWE INFORMACJE ORGANIZATOREM SZKOLENIA
• 8 PORT RS232 PCI CARD D ESCRIPTION
• 80•IN•30 OUDEREN OP WEG NAAR 2030 PROGRAMMA VAN
• C UANTO MÁS TARDE PEOR M AMÁ ¿PUEDO QUEDARME
• KEY MESSAGES BOARD MEMBERS WANT TO HEAR THE CREATION
• TAX DEDUCTIBLE DONATION ACKNOWLEDGEMENT THANK YOU FOR DONATING YOUR