UNDERSTANDING VOLTAMMETRY APPENDIX APPENDIX SIMULATION OF ELECTRODE PROCESSES THE
10 NEVER AGAIN UNDERSTANDING THE PAST TOTECHNOLOGY MEMORANDUM OF UNDERSTANDING ADVICE REGARDING THE
THEME UNDERSTANDING COMMUNICATION ACTIVITY THE BRIALLE ALPHABET
UNDERSTANDING THE SOCIAL SCIENCES AS A LEARNING AREA
(RE)UNDERSTANDING EDUCATOR ACCOUNTABILITY PSEUDO VS AUTHENTIC ACCOUNTABILITY RANDY L
1 INTRODUCTION YOUR KNOWLEDGE AND UNDERSTANDING OF YOUR LOCAL
Chapter 1
Understanding Voltammetry Appendix
Appendix
Simulation of Electrode Processes
The purpose of this appendix is to provide an insight into how simple numerical simulations of one dimensional diffusion problems can be carried out.
A.1 Fick’s First and Second Laws
The voltammetry experiment conducted in quiescent solution considers mass transport of species by diffusion only. The flux of a species through a solution is mathematically described by Fick’s First Law [1] which is described in Chapter 3. This is as follows:
Fick’s First Law: ![]() (A1)
(A1)
where j is the flux, D is the diffusion coefficient, c is the concentration of a species and x is the spatial coordinate. Equation (A1) allows us to calculate the passage of flux in a steady-stat system, where the concentration gradients are invariant in time. However the nature of the electrochemical systems is such that concentration gradients are usually constantly changing. Fick derived a second law (Chapter 3) to describe this change of concentration with time, t, in the form of a second order differential equation:
Fick’s Second Law:
![]() (A2)
(A2)
As stated, these laws only describe a one-dimensional system. Generalised to three Cartesian directions, the 2nd law becomes:
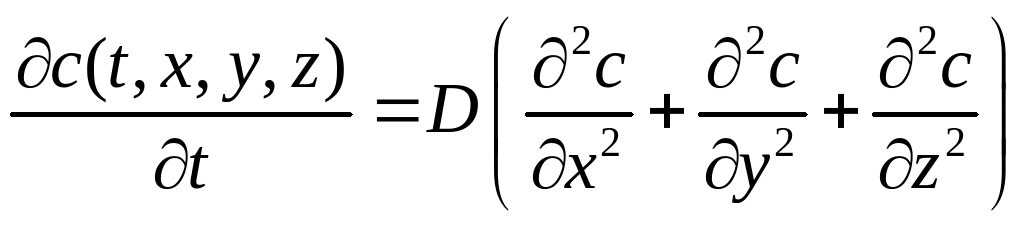 (A3)
(A3)
A.2 Boundary Conditions
The solution to a second order differential equation may only be solved with the introduction of boundary conditions. In physical terms this represents the restrictions imposed on the electrolyte concentration (Dirichlet boundaries) or its derivative (Neumann boundaries- e.g. flux) in time and space by the experiment.
A.3 Finite Difference Equations
Mass transport equations are partial differential equations.
The concentration is a function of both distance, x and time,
t. Since our model of cyclic voltammetry (Chapter 4) demands
only one dimension in space, we can approximate this function as
discrete points in time and in space. This process is known as
‘discretisation’. Points in the x-direction are
assigned values of j = 0, 1, 2, 3….NJ spaced Δx
apart whilst those in the time are assigned values of l =
0, 1, 2, 3….Nl, spaced Δt apart. Hence any
instantaneous point concentration is specified by values of l
and j and we use the notation
![]() to
emphasise this. Finite difference equations are approximations of
partial derivatives in terms of discretised values. Those applicable
to our model are:
to
emphasise this. Finite difference equations are approximations of
partial derivatives in terms of discretised values. Those applicable
to our model are:
![]() (upwind differencing – concentration gradient at j + ½)
(upwind differencing – concentration gradient at j + ½)
![]() (downwind
differencing – concentration gradient at j - ½)
(downwind
differencing – concentration gradient at j - ½)
and ![]() (central
differencing – concentration gradient at j )
(central
differencing – concentration gradient at j )
The upwind and downwind differencing equations may be combined to produce an approximation for the second derivative.
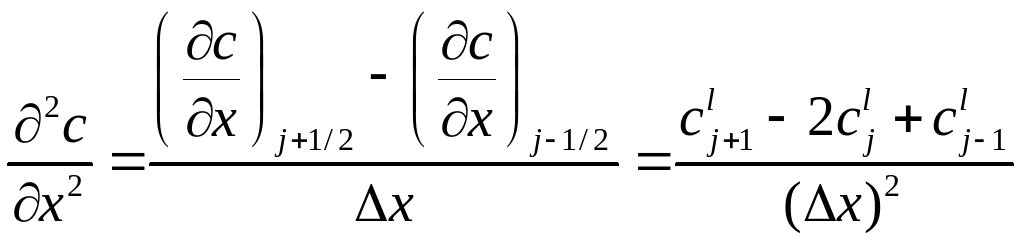 (A4)
(A4)
Also for the derivative of concentration with time:
![]()
A.4 Backward Implicit Method
The Backward Implicit (BI) method [2,3] is a powerful system for calculating a set of concentration, in a one or two – dimensional spatial system. Because the concentration profile is solved vector-by-vector, only three nodes can be spanned within one spatial coordinate, so limiting general application. However, it is well suited to producing quick solution to 1D problems. The BI method involves the assimilation of a linear system of equation by discretisation of the mass transport equation, which can be re-arranged to form a matrix equation and subsequently solved.
To exemplify the use of the BI method, we will simulate the application of a potential step to a
![]() (A5)
(A5)
redox couple, such that at a time, t > 0, the A species at the electrode surface is fully oxidised to B. The A species occupies the x-coordinate between x = 0 and x = δ, where δ is a diffusion layer thickness large enough that semi-infinite diffusion operates, i.e.
![]()
This problem was considered in Chapter 3. The mass transport for the A species is:
![]()
The BI methods follows the following four steps:
Conversion of MT equations to finite difference form:
![]()
where
![]() and
and
![]() is assigned arbitrarily
is assigned arbitrarily
2. Rearrangement to give a set of linear equations:
![]()
![]()
where ![]()
3. Application of boundary conditions:
The boundary conditions applicable to this simulation are
(a) ![]()
![]()
![]()
(b) ![]()
![]()
![]()
(c) ![]() (A species fully oxidised at surface)
(A species fully oxidised at surface)
![]()
The introduction of boundary conditions at the diffusion layer limit to the finite difference equations gives:
![]()
But since
![]()
![]()
At the electrode surface,
![]()
But since
![]()
![]()
4. Arrangement of linear equations into a matrix equation

With the initial values of [A] set to their initial bulk values, this matrix equation can be solved sequentially to give a concentration vector at every time node. After many iterations, the system will become steady state, i.e. the concentration profile will be invariant with each new iteration. Equations of the above form can be solved using The Thomas Algorithm [4,5] devised by Laasonen [6] before the invention of computer. This allows the solution of a tridiagonal matrix equation:
![]()
to be found implicitly, where
![]() is
unknown,
is
unknown,
![]() and
and![]() being
vectors of
being
vectors of
![]() elements and
elements and
![]() being a tridiagonal matrix of the form:
being a tridiagonal matrix of the form:
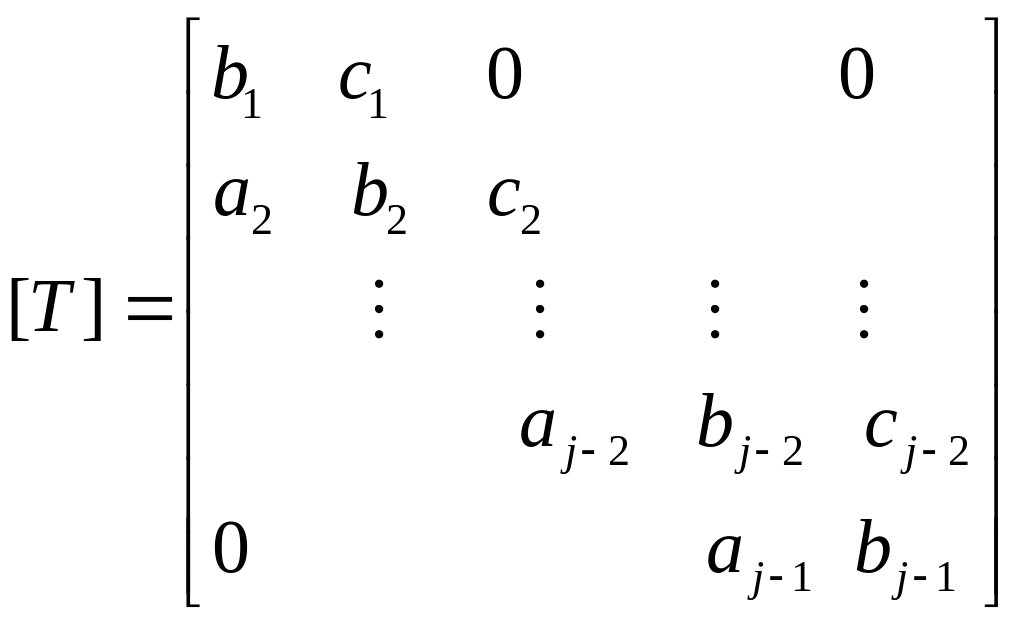
In solution to the mass transport equations,
![]() represents
the set of known concentrations
represents
the set of known concentrations![]() ,
and
,
and
![]() ,
the unknown concentrations
,
the unknown concentrations
![]() which are to be calculated in the next pass of the Thomas algorithm.
Once calculated, the vector
which are to be calculated in the next pass of the Thomas algorithm.
Once calculated, the vector
![]() is
set to
is
set to![]() ,
and the new matrix
,
and the new matrix
![]() calculated.
This process is repeated up to the end time of the simulation. In
this way the concentration versus distance profile can be discussed
as a function of time.
calculated.
This process is repeated up to the end time of the simulation. In
this way the concentration versus distance profile can be discussed
as a function of time.
A6. Conclusion
This appendix has introduced some elementary theory behind the mathematical modelling of electro-active species in solution, as well as its implementation to produce computational simulations.
A7. References
[1] A. Fick, “Uber Diffusion”, Poggendorff's Annel. Physik. 94, (1855), 59
[2] J.L. Anderson, S. Moldoveanu, J. Electroanal. Chem., 179, (1984), 109
[3] R.G.Compton, M.B.G. Pilkington, G.M. Stearn, J. Chem. Soc., Faraday Trans 1, 84, (1988), 2155
[4] L.H. Thomas, Elliptical problems in linear difference equations over a network, Watson Sci. Comput. Lab. Rept. Columbia University, New York, 1949
[5] G.H.Bruce, D.W. Peaceman, H.H. Rachford, J.D. Rice. Trans. Am. Inst. Min. Engrs, 198, (1953), 79
[6] P. Laasonen, Acta Math., 81, (1949), 30917
11 GARCÍA LANDA – UNDERSTANDING MISREADING UNDERSTANDING MISREADING HERMENÉUTICA
13 UNDERSTANDING OF LIMITS AND DIFFERENTIATION AS THRESHOLD CONCEPTS
1595542239UNDERSTANDING_LEXICAL_STRUCTURE_(corrected)
Tags: appendix appendix, this appendix, appendix, simulation, understanding, electrode, voltammetry, processes
- D1 FORM QUALITY ASSURANCE HANDBOOK 202021 ACCREDITATION OR RECOGNITION
- MEADOW LANE ELEMENTARY PARENT INVOLVEMENT POLICY DEAR
- GTBTNBDI82 3 NOTIFICATION LA NOTIFICATION SUIVANTE EST
- 3 ДЕЛО № 5149121082020 ПОСТАНОВЛЕНИЕ ПО ДЕЛУ ОБ АДМИНИСТРАТИВНОМ
- OŚWIADCZENIE O PRZYNALEŻNOŚCI LUB BRAKU PRZYNALEŻNOŚCI DO GRUPY KAPITAŁOWEJ
- ANKARA ÜNİVERSİTESİ DİL VE TARİHCOĞRAFYA VAKÜLTESİ DOĞU DİLLERİ DERGİSİ
- PRVA STATISTIČNA OBJAVA ŠT 1622005 FIRST RELEASE NO 1622005
- THE IMPORTANCE OF LOOKING TOWARD THE FUTURE AND BUILDING
- CURRICULUM VITAE PHIL S BARAN APPOINTMENT SCRIPPS RESEARCH PROFESSOR
- OBEC STARÉ HODĚJOVICE ZASTUPITELSTVO OBCE STARÉ HODĚJOVICE OBECNĚ ZÁVAZNÁ
- CONTRATO CON GALERÍA COMERCIAL PARA EXPOSICIÓN ESPECÍFICA ESTE CONTRATO
- DATE 041521 BOARD OF TRUSTEES MEETING FROM EXECUTIVE COMMITTEE
- EUROPEAN PARLIAMENT 2009 2014 COMMISSION{PECH}COMMITTEE ON FISHERIESCOMMISSION REFPROC20130136REFPROCREFTYPEPROC(COD)REFTYPEPROC
- DOCUMENTATION FOR FILLED METEOROLOGY DATA CONTACT DR DANIEL RICCIUTO
- COUNTRY CONTACT PERSON NAME ORGANISATION TELEPHONE NUMBER EMAIL ADDRESS
- BANNER FINANCE AND REPORTING GUIDE FOR DEPARTMENTAL
- LA MARCA LA MARCA ES EN REALIDAD AQUELLO QUE
- LES TRES CONJUGACIONS EN PRESENT D’INDICATIU LA PRIMERA CONJUGACIÓ
- »FUNKCIJE MOKRIŠČ ZA ŽIVLJENJE IN RAZVOJ« VABILO NA POSVET
- GARAŽE U VLASNIŠTVU GRADA PAZINA ADRESA M2
- INTERACCIÓN ROLES Y ETAPAS DE DESARROLLO GRUPAL EL PROCESO
- VALIDATION REQUIREMENTS FOR PLANNING AND OTHER APPLICATIONS SUBMITTED UNDER
- AMUR ASOCIACION MUTUAL RURALISTA LLEVARÁN “AUTORIZACIÓN PREVIA” AQUELLOS MEDICAMENTOS
- BERANDA TENTANG KAMI PROFIL UNIVERSITAS PGRI
- NZQA UNIT STANDARD 1980 VERSION 9 PAGE 3 OF
- GOBIERNO DE LA RIOJA WWWLARIOJAORG AUTOBAREMACIÓN DESARROLLO PROFESIONAL GRUPOS
- MARI ÁLVAREZ LIRES É DOUTORA EN QUÍMICA CATEDRÁTICA DE
- FORMULARZ APLIKACYJNY FORMULARZ PROSIMY WYPEŁNIAĆ CZYTELNIE !!!
- SSTS EXPERIENCE DOCUMENTATION FORM FOR INDIVIDUALS CERTIFIED ON OR
- INVESTIGACIÓN EN HETEROCIGOTAS DE LA GANGLIOSIDOSIS GM2 TIPO II
2 Consejo Permanente de la Oeaserkxvi Organización
CAUSE NO § IN THE DISTRICT COURT
REMARKS BY HE AMBASSADOR CHEN YUMING AT THE SINOSWEDISH
WICKLOW COUNTY COUNCIL VACANCY REFUNDRELIEF APPLICATION FORM 2017 IF
 36 KNOWL ORG 25(1998)NO12 B HJØRLAND INFORMATION RETRIEVAL TEXT
36 KNOWL ORG 25(1998)NO12 B HJØRLAND INFORMATION RETRIEVAL TEXTMETROPOLITAN MEDICAL RESPONSE SYSTEM ALBUQUERQUE AREA HOSPITAL MEETING FEBRUARY
LOS ANTIDEPRESIVOS PARA EL DOLOR CRÓNICO LOS ANTIDEPRESIVOS LA
“REPASO DE LAS OPERACIONES A DECLARAR EN EL MODELO
 EL CATALÀ ALS TELÈFONS MÒBILS A PARTIR DELS
EL CATALÀ ALS TELÈFONS MÒBILS A PARTIR DELSNOMBRE CALENTAMIENTO PARTE I COMPLETE CON EL
POLÍTICA DE USO DE TELÉFONOS CELULARESDISPOSITIVOS ELECTRÓNICOS PREPARADO POR
 STATE OF TENNESSEE ELECTRICAL WIRING PERMITS WIRING PERMITS CAN
STATE OF TENNESSEE ELECTRICAL WIRING PERMITS WIRING PERMITS CANMARTES 22 DE NOVIEMBRE DE 2016 DIARIO OFICIAL (SEGUNDA
22 POSLOVNI BROJ LXXXVIP112300959 POSLOVNI BROJ LXXXVIP112300959 U I
 my Problem is Think About Solutions What
my Problem is Think About Solutions What JAK ODWOŁAĆ SIĘ DO PREZESA ZAKŁADU UBEZPIECZEŃ SPOŁECZNYCH OD
JAK ODWOŁAĆ SIĘ DO PREZESA ZAKŁADU UBEZPIECZEŃ SPOŁECZNYCH OD ANEXO 11 PROCEDIMIENTOS E INDICADORES ENTOMOLÓGICOS PARA TOMA DE
ANEXO 11 PROCEDIMIENTOS E INDICADORES ENTOMOLÓGICOS PARA TOMA DEEL BAUTISMO DE LOS NIÑOS CONTENIDO PROLOGO CAPITULO I
MOCIÓN PARA LA REACTIVACIÓN DE LA LEY DE PACTO
2 FACSIMILE DELLA DOMANDA DI AMMISSIONE DA INOLTRARE POSSIBILMENTE