FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH

32 CENTRALE PERSONER I UDDANNELSEN VIGTIGE FUNKTIONER I SPECIALLÆGEUDDANNELSEN
75 STRATEGI FÖR TRYGGANDE AV SAMHÄLLETS LIVSVIKTIGA FUNKTIONER STRATEGI
BYTE AV LÄKEMEDELSKASSETT OCH BATTERIBYTE GRUNDFUNKTIONER STARTA

FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH
INSTRUKTION FÖR UPPDELNING PÅ HUVUDFUNKTIONER VID SLU
PUMPENS FUNKTION BESKRIVNING AV KNAPPAR TECKENFÖNSTER OCH FUNKTIONER

Funktioner, speciellt linjära funktioner

Funktioner.

Ex.1. Telefonräkning. Antag kvartalsavgiften är 250 kr och priset per markering 20 öre. Låt x vara antal markeringar under ett kvartal och y totala kostnaden räknad i kronor.

Värdet av y beror på värdet av x.

eller y är en funktion av x. Vi skriver .

x är den oberoende variabeln och y den beroende variabeln.

Hur y beror på x ges av funktionens ekvation .

Denna funktion kan beskrivas med dess graf.

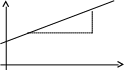FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH y

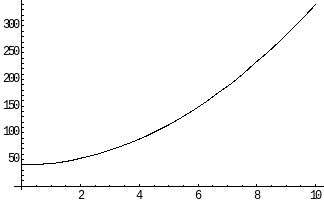O FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH bservera att om x = 0 är y = 250 samt att
för varje gång x ökar med ett ökar y med 0,20. 200
I detta exempel kan vi låta x öka med 1000 vilket gör att
y ökar med 200. (0 ; 250) 1000

y är en linjär funktion av x
x
Att alla funktioner ej behöver vara linjära ser man av följande exempel:

Ex.2 För att måla en kvadratisk yta med sidan x (m) har Olle en fast betalning om 40 kr plus 3 kr per kvadratmeter. Totala betalningen y (kr) är en funktion av kvadratens sida x.

Funktionens ekvation kan skrivas:

vars graf ser ut såhär:

Här ökar ej y linjärt med x.

Vi har en kvadratisk funktion och
denna typ av kurva kallas en parabel

Man kan också kalla den en andragrads-
-kurva

M FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH an kan betrakta en funktion som en ”maskin” som gör något med x:

x x

y y

x multpliceras med 0,20 x kvadreras

sedan adderas 250 kvadraten multipliceras med 3

till sist adderas 40

Resultat: Resultat:

Observera i vilken ordning operationerna utförs.

Exempel på en linjär och en kvadratisk funktion har vi i fysiken vid rörelse med konstant acceleration (likformigt accelererad rörelse). Låter vi tiden t vara den oberoende variabeln kan hastigheten v och sträckan s beskrivas som funktioner av t genom:

och

v₀ är här begynnelsehastigheten och a accelerationen.

En annan typ av funktioner är de exponentiella, som vi möter då vi vill beskriva exempelvis ett kapitals tillväxt med tiden eller ett radioaktivt sönderfall.

Ex.3 Antag vi sätter in 400 kr (den 31/12) på banken ett år mot 4% ränta. Om vi vill ha reda på hur stort kapital vi har efter 10 år och räknar på vanligt vis, skall vi räkna ur räntan varje år och sedan lägga till denna, dvs vi måste utföra 10 multiplikationer och lika många additioner.
Lättare är då att tänka att vi i början av varje år har 100% av kapitalet och att det sedan läggs till 4% så att vi har 104% = 1,04 av det ursprungliga kapitalet. För varje år som går multiplicerar vi med förändringsfaktorn 1,04. Efter 1 år har vi kr efter 2år kr och efter 10 år kr.
Allmänt om y är kapitalet efter x år gäller att
,
en funktion, som beskriver hur kapitalet växer med ”ränta på ränta”

Ex.4 Antag att vi har 600 g av ett radioaktivt ämne, som sönderfaller så att varje år försvinner 11% av ämnet. Detta innebär att efter varje år återstår 89% = 0,89 av den ursprungliga mängden. För varje år som går multiplicerar vi med förändringsfaktorn 0,89. Om då y år återstående mängden (i g) efter x år blir funktionens ekvation:

K FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH urvorna till funktionerna i ex 3 och 4 blir (naturligtvis har vi olika enhet på y-axeln i de två fallen):

Vi har ovan beskrivit några matematiska modeller. Försök att beskriva nedanstående exempel som funktioner. Tala om vad dina variabler står för (ange enhet) och ange vilken typ av funktion du får.

För att tillverka en sak behövs en fast investering på 10 000 kr och sedan kostar det 500 kr att tillverka en enhet. Beskriv totala tillverkningskostnaden som funktion av antalet tillverkade enheter.
Om man hyr en bil betalar man 18 kr per körd mil och 200kr i dygnsavgift. Vilken blir den totala kostnaden att hyra bil en dag?
Under en dag regnar det 40mm på en rektangulär tomt vars ena sida är dubbelt så stor som den andra. Beskriv totala volymen vatten, som faller ned på en sådan tomt.
En bakteriekultur innehåller från början 1500 bakterier och den växer sedan med 1,3 % varje timma. Beskriv hur antalet bakterier växer med tiden.

Funktioner.(forts.)

Antag vi har 500 bakterier i en odling och att dessa får växa ohämmat med en tillväxthastighet som är 3% per timme. Den relativa tillväxthastigheten är alltså konstant och vi har en så kallad exponentiell tillväxt där tillväxtfaktorn är 1.03. Antalet bakterier växer med 3% eller till 103% av det ursprungliga antalet varje timma. Låt vara antalet bakterier efter x timmar. Sambandet mellan y och x kan då skrivas

. eller .

N FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH är så är och då är o.s.v. En värdetabell och graf för funktionen får följande utseende:

x f(x)

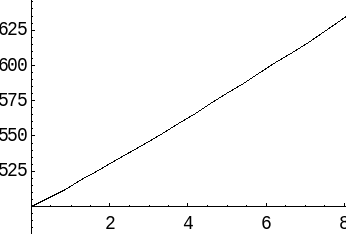
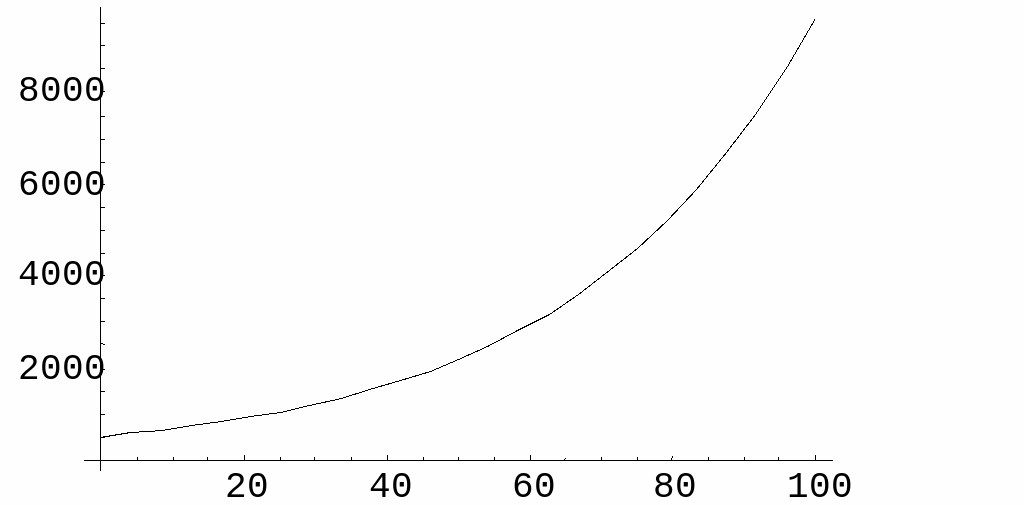
V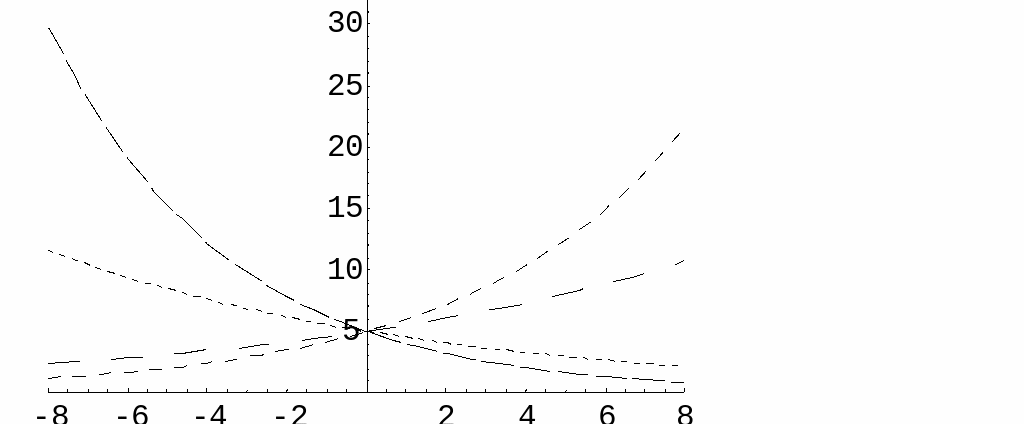 FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH i skall inte låta lura oss av kurvan i detta område ser nästan linjär ut. Lägg också märke till att y-axeln är avhuggen. Låter vi antalet år sträcka sig upp till 100 får vi istället följande kurva, där den exponentiella tillväxten framgår tydligare. Hur liten den procentuella tillväxten än är "vinner" alltid en exponentiell funktion över en andragradsfunktion, bara en tillräckligt lång tid får gå.

FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH

I diagrammet till höger har funktionen ritats upp för de olika förändringsfaktorerna samt 0.9. Vilken kurva hör till vilken funktion?

Lägg också märke till att och inte är varandras spegelbilder i y-axeln. Däremot är och symmetriska med avseende på y-axeln.

Olika typer av funktioner:

kallas en linjär funktion
är en kvadratisk eller en andragradsfunktion
är en tredjegradsfunktion
är en exponentialfunktion
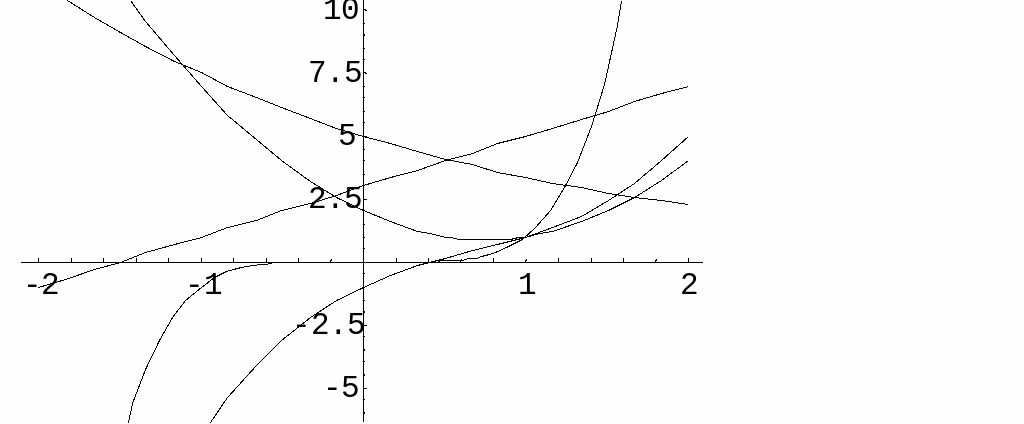är en potensfunktion

Funktionernas grafer har ritats upp i diagrammetovan. Försök att ta reda på vilken som är vilken och fyll i dem med olika färger.

Uppgift: Svar:

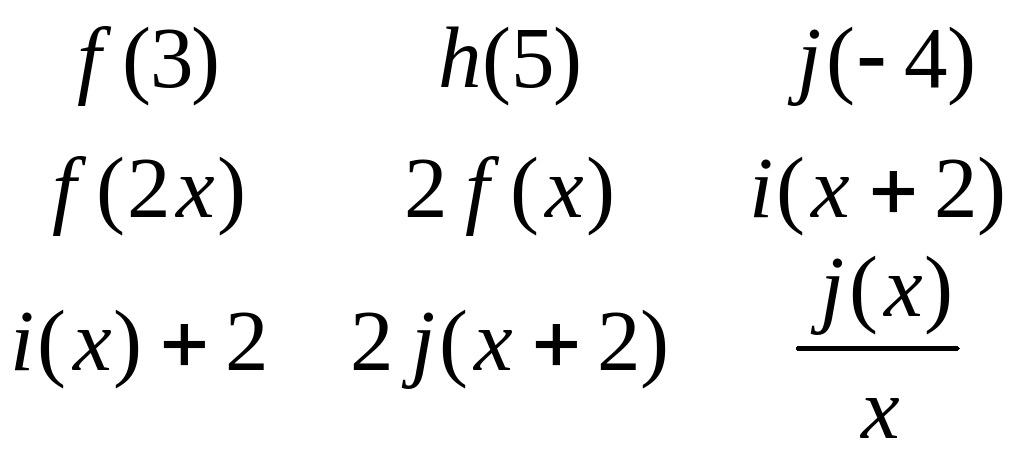
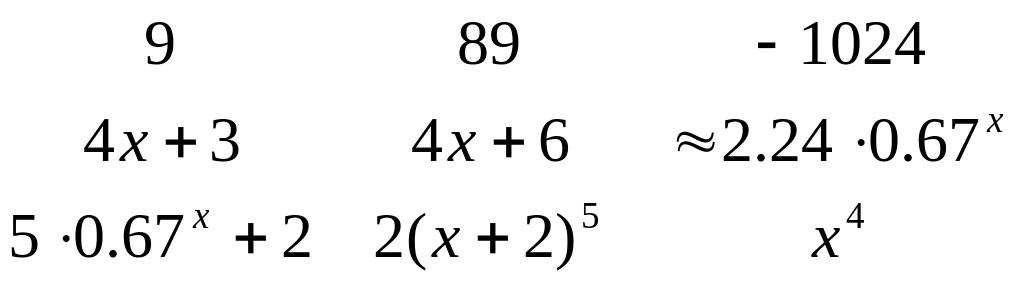
Bestäm FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH

Låt vara positionen (läget) vid tidpunkten x för en kropp som faller fritt. Vi antar att vi jobbar med SI-enheterna m och s. Då är , , och .Kroppen har alltså fallit 46m under de två sekunderna och medelhastigheten blir m/s. Jämför med följande diagram:

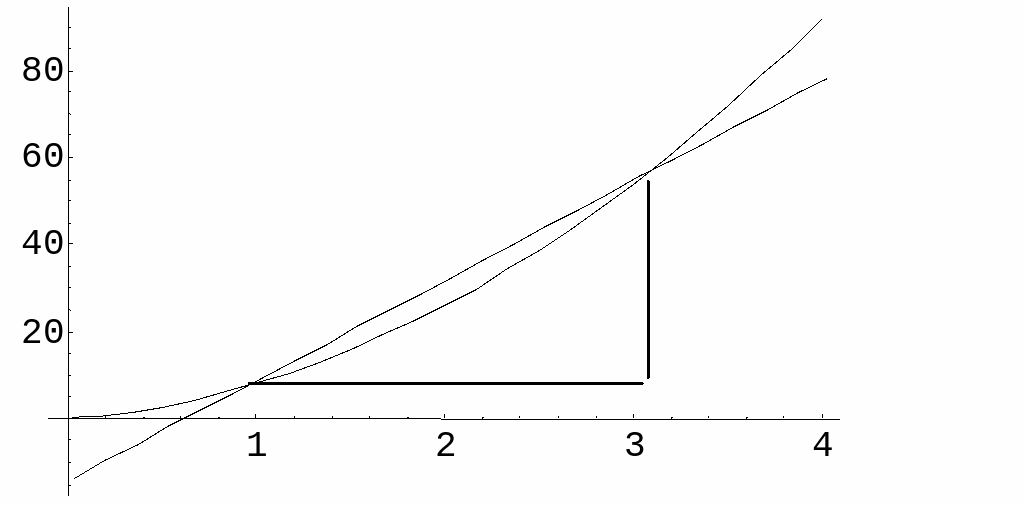FUNKTIONER EX1 TELEFONRÄKNING ANTAG KVARTALSAVGIFTEN ÄR 250 KR OCH blir alltså k-värdet för den linje som förbinder punkterna (1;8) och (3;54). Denna linje kallas en sekant

f till kurvan .

x

SKEMA TIL INDIVIDUEL AFTALE OM OPGAVER OG FUNKTIONER FOR

Tags: antag kvartalsavgiften, funktioner.(forts.) antag, antag, kvartalsavgiften, telefonräkning, funktioner