MATRIX FUNCTIONS 1 WE CAN EASILY DEFINE A NATURAL

QUESTION & ANSWER (Q&A) MATRIX ON IMPLEMENTATION OF
2 MATRIX ALGEBRA IN THIS SECTION YOU WILL LEARN
201605-0324-basic-fatigue-management-audit-matrix-bfm

22 122121 GENERAL EDUCATION REPORTING MATRIX CONTACT DR PAULA
4 UK AIDMATCH SCIAF PROGRAMME RISK MATRIX RISK LIKELIHOOD
9 LEASTSQUARES JOINT DIAGONALIZATION OF A MATRIX SET BY

Matrix functions

Matrix functions

1. We can easily define a natural power of a square matrix X as a product:

For a non-singular matrix, a negative power can be defined as a corresponding positive power of the matrix inverse:

X^–n = (X^–1)ⁿ

or, alternatively, as the matrix inverse of the positive power:

X^–n = (Xⁿ)^–1

Exercise: Demonstrate that the two definitions are equivalent.

The zeroth power of any matrix is the identity matrix by definition:

X⁰ = I

Exercise: Demonstrate the following properties of matrix powers:.

XⁿX^m = X^n+m

(Xⁿ)^m = X^nm

3. If y is an eigenvector of matrix X: Xy = y, then X²y = XXy = Xy = Xy = ²y. Analogously, for any power: Xⁿy = ⁿy. Therefore, the n-th power of matrix X has the same eigenvectors as the original matrix X, with the corresponding eigenvalues being ⁿ. This is also true for any negative power, including the matrix inverse: X^–1y = y  XX^–1y = Xy  Xy = (1/)y.

A diagonalizable matrix X can be expressed as follows (similarity transformation):

X = TT^–1

where  = diag(₁,₂,..._N) is the diagonal matrix of eigenvalues and T is the eigenvector matrix (column by column). Then, for the X² matrix we obtain:

where ^ = diag(₁²,₂²,..._N²). In the case of normal matrices (X^†X = XX^†), the eigenvectors are orthogonal: T^–1 = T^†. Analogously, any power Xⁿ can be expressed as follows:

Xⁿ = TⁿT^–1

ⁿ = diag(₁ⁿ,₂ⁿ,..._Nⁿ).

4. If a given real function can be expressed as a Taylor series:

where

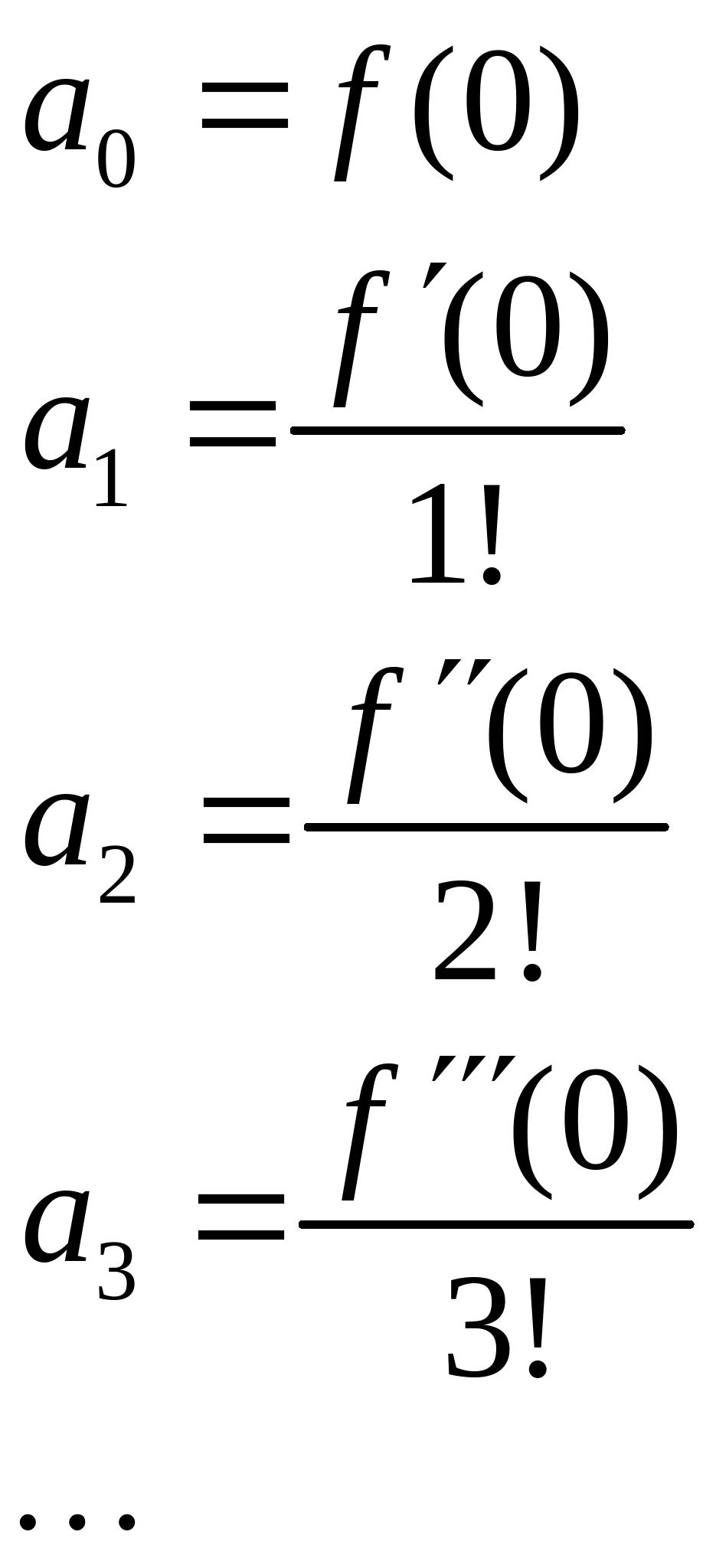
MATRIX FUNCTIONS 1 WE CAN EASILY DEFINE A NATURAL

we can construct a similar power series substituting the scalar argument x by a square matrix X:

This is a definition of function f of a matrix X.

For instance, the exponent of matrix X will be given by the following series:

5. The above Taylor expansion can be used as such to iteratively compute a matrix function, but for diagonalizable matrices it is usually more efficient to employ the following algorithm:

a. Diagonalize matrix X, obtain the matrix of eigenvectors T and the diagonal matrix of eigenvalues . If X is not a normal matrix, we will also need to invert T. This gives a similarity transformation X = TT^–1, where  = diag(₁,₂,..._N).

b. The exponent of matrix X is given by the following expression:

MATRIX FUNCTIONS 1 WE CAN EASILY DEFINE A NATURAL

The latter formula gives us a non-iterative method of calculating exp(X) through diagonalization. In general, any matrix function can be calculated this way:

f(X) = T diag(f(₁), f(₂),... f(_N))T^–1.

Obviously, f(X) has the same eigenvectors as the original matrix X, with the corresponding eigenvalues being f().

6. The square root X^1/2 of matrix X is defined through the expression (X^1/2)² = X. The calculation of X^1/2 can be also carried out by way of the diagonalization technique:

Exercise: Demonstrate that the above formula indeed yields X^1/2.

6. The inverse square root X^–1/2 of matrix X is defined through the expression (X^–1/2)² = X^–1. The calculation of X^–1/2 can be done analogously:

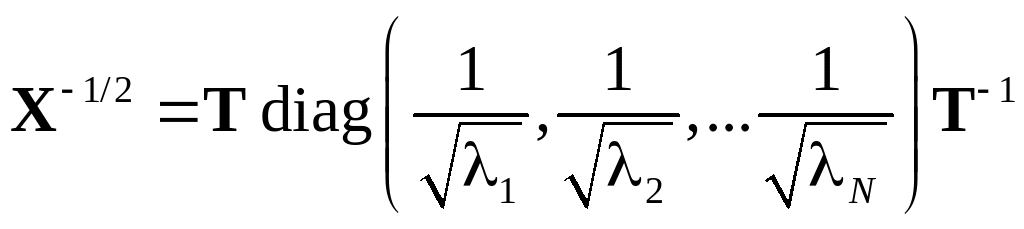
MATRIX FUNCTIONS 1 WE CAN EASILY DEFINE A NATURAL

Of course, this is only possible if all eigenvalues are non-zero. Otherwise, X is singular and X^–1/2 does not exist. Note that the functions or can not be represented by Taylor series. Nevertheless, the above algorithms work.

The inverse square root plays a crucial role in the Löwdin orthogonalization method.

7. Note that if matrix X is Hermitian, all its powers Xⁿ and matrix functions f(X) will be also Hermitian. This refers, in particular, to matrix inverse X^–1, matrix square root X^1/2, and the inverse square root X^–1/2.

ABSTRAK PEMBUATAN ALSIC METAL MATRIX COMPOSOITES DENGAN METODE LANXIDE
ACCOMMODATIONS MATRIX FOR DAILY ACTIVITIES READ WRITE HDWR
ACCOUNTING MATRIX STRANDS CONCEPTUAL PROCESSING REPORTING INTERPRETATION

Tags: define a, natural, functions, easily, define, matrix