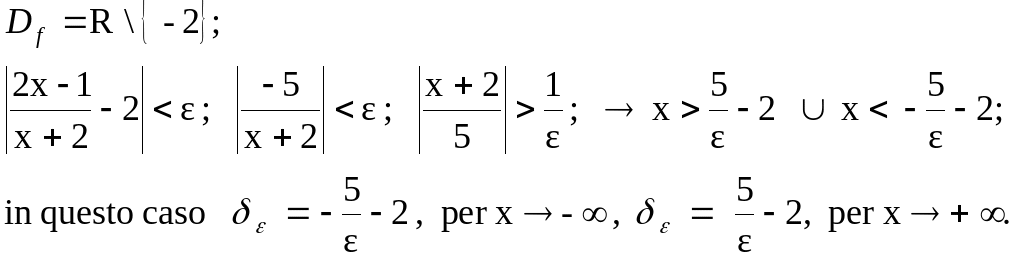35 LIMITI 1 LIMITE FINITO IN UN PUNTO 2

35 LIMITI 1 LIMITE FINITO IN UN PUNTO 2
MARIE CURIE SUPPORTING YOUNG PEOPLE WITH LIFELIMITING CONDITIONS FURTHER
NAME LIBERTY SCIENCE CENTER FIND THE LIMITING NUTRIENT

---

NAME[KEY] DATE PERIOD WS LIMITING REACTANT & PERCENT YIELD
NOTES LIMITING REACTANTS & PERCENT YIELD PRACTICE WS 1
UNITÀ DI APPRENDIMENTO “REGOLE LEGGI LIMITI E CONFINI” (SECONDARIA

---

LIMITI

LIMITI

1. Limite finito in un punto

2. Limite infinito in un punto

3. Limite finito all’infinito

4. Limite infinito all’infinito

5. Limiti da destra e da sinistra
   Nota bene 1°

6. Esempi di riepilogo
   Nota bene 2°

7. Limite per eccesso e per difetto

8. Limiti fondamentali

1 . Limite finito in un punto

Data la funzione f(x) : D_f → C_f , con D_f R e C_f R, considerato il punto x_{0 ,} con x₀ punto d’accumulazione di D_f , si definisce limite finito in x₀ il numero reale l che soddisfa alla seguente condizione:

l è limite della funzione f(x) per x che tende ad x₀, e si scrive , se , tale che , .

N.B.: in questa definizione è interessante considerare ε ‘piccolo a piacere’, cioè ε → 0.

Esempi

Verificare l’esistenza di un limite secondo la definizione, significa risolvere la disequazione indicata, in questo caso , e trovare come risultato un intorno di x₀ , privato al più di x₀.

1.a Data la funzione , verifica che .

D_f = R \ {1} ;

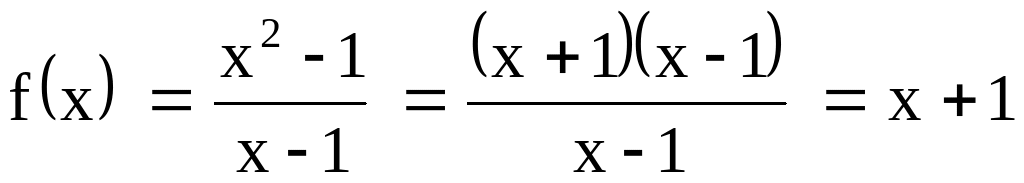
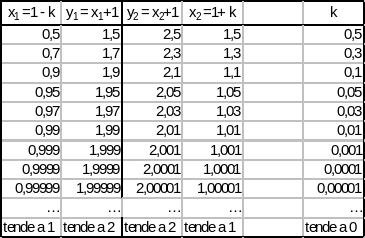
Verifica empirica:

Verifica secondo la definizione:

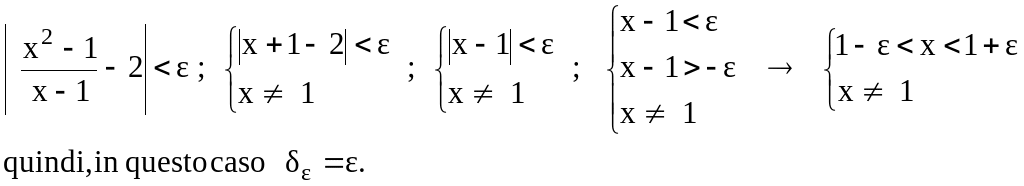
Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di x₀ = 1, privato di x₀ = 1.

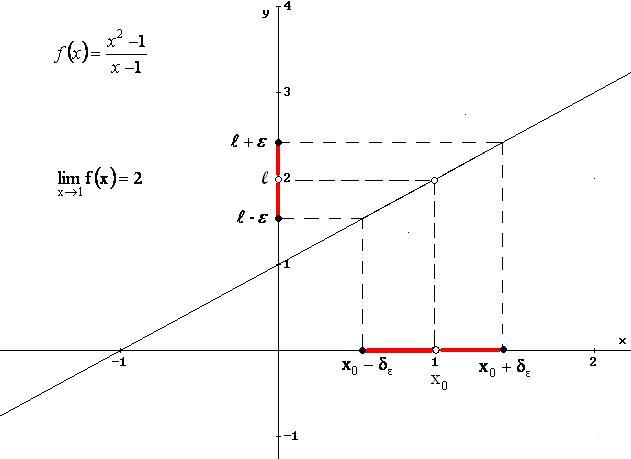
1.b Considera la funzione dell’esempio 1.a, e verifica che
l’affermazione è falsa.

Infatti, applicando la definizione, si ottiene come risultato un intorno
completo di 2, anziché un intorno di x₀ = 1, privato di x₀ = 1:

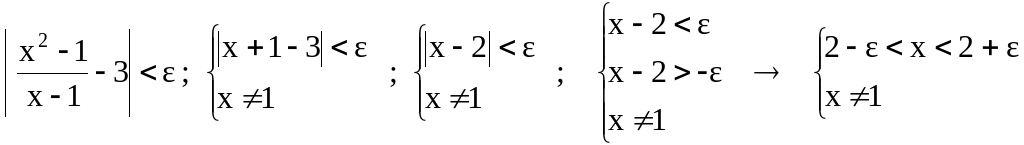
2 . Limite infinito in un punto

Data la funzione f(x) : D_f → C_f , con D_f R e C_f R, considerato il punto x_{0 ,} con x₀ punto d’accumulazione di D_f , si dice che il limite della funzione f(x), per x che tende ad x₀, è infinito, e si scrive ,

se , tale che .

N.B.: a) in questa definizione è interessante considerare M ‘grande a piacere’, cioè M → +  .

b) in particolare, se il limite è + -  ), basta che sia verificata la disequazione f(x) > M
( f(x) < - M ) .

c) la definizione vale per , tuttavia per semplicità conviene prendere .

Questo tipo di limite implica l’esistenza di asintoto verticale di equazione x = x₀.

Esempio

Verificare l’esistenza di un limite secondo la definizione, significa risolvere la disequazione indicata, in questo caso , e trovare come risultato un intorno di x₀ , privato al più di x₀.

2.a Data la funzione , verifica che .

D_f = R \ {0} .

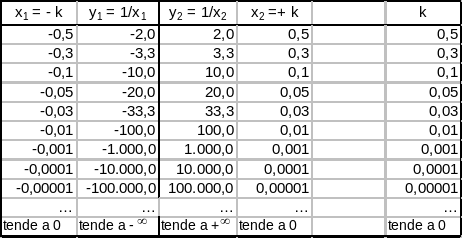
Verifica empirica:

Verifica secondo la definizione:

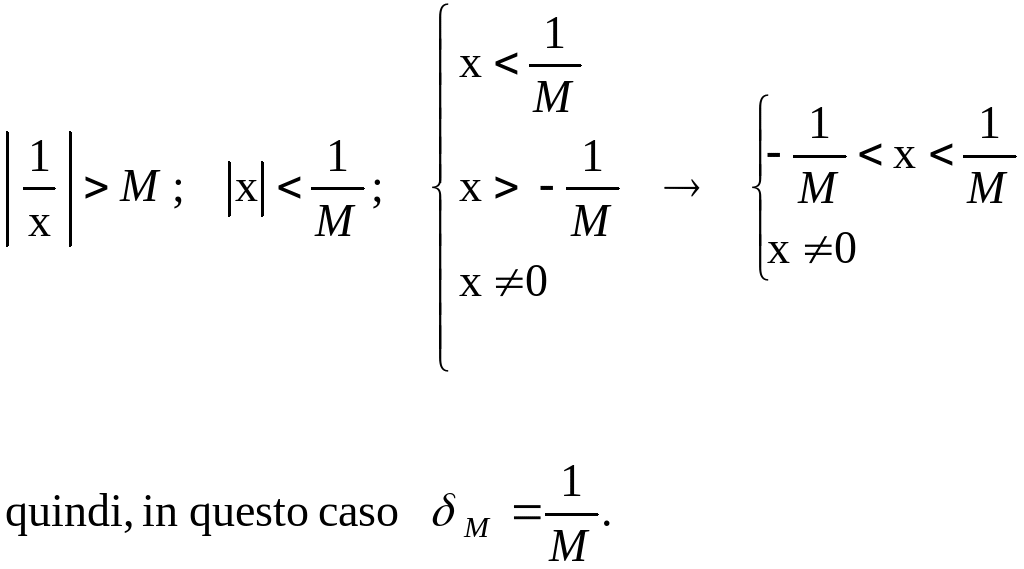
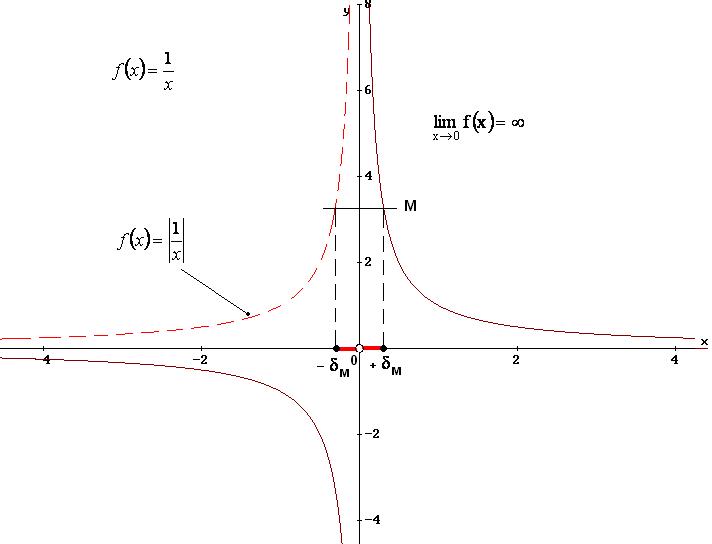
Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di x₀ = 0, privato di x₀ = 0.

La funzione ammette asintoto verticale di equazione x = 0.

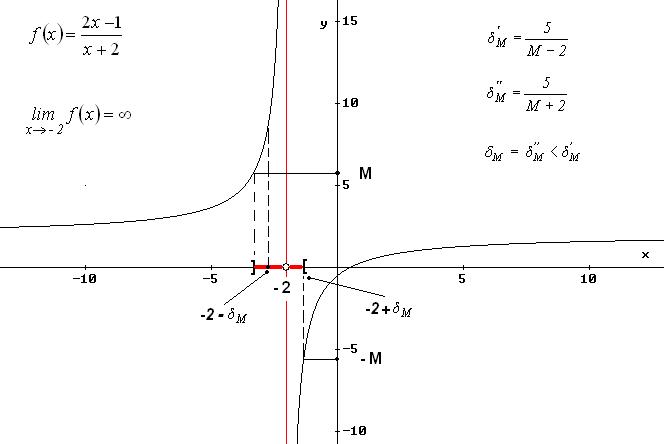
2.b Data la funzione , verifica che .

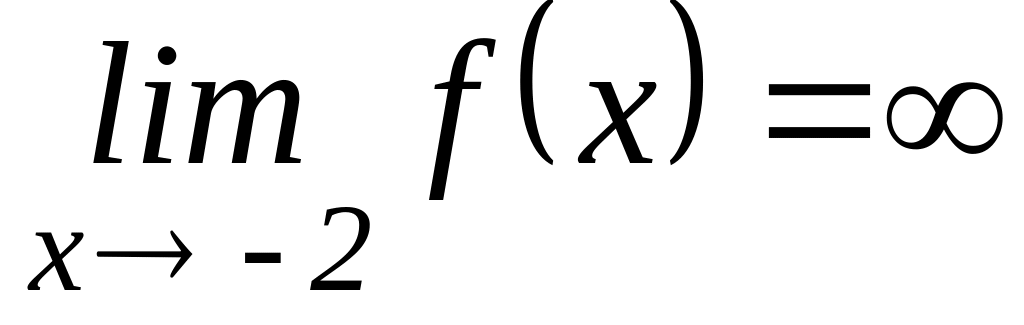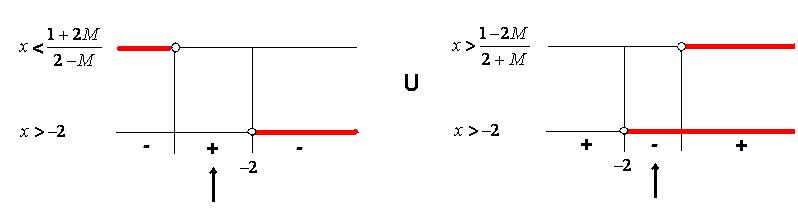
quindi, la disequazione è verificata per

Osserva che per M ‘ molto grande ’, per esempio M = 1000, si ha:

Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di x₀ = - 2, privato di x₀ = - 2.

Determino δ_M :

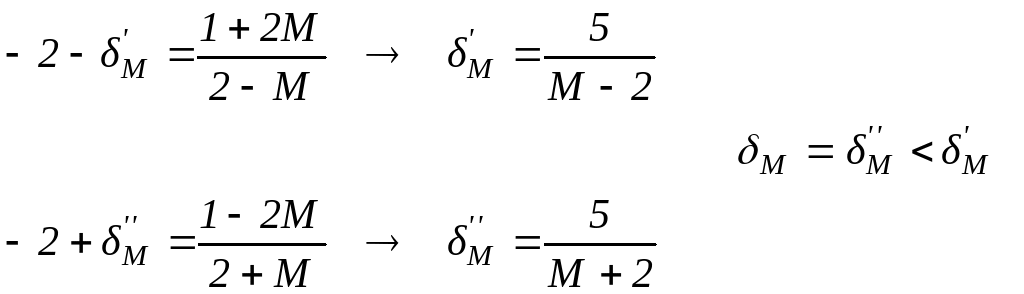
Si può concludere, in modo più raffinato, che , e che l’ intorno di x₀ = - 2, privato di x₀ = - 2 è .

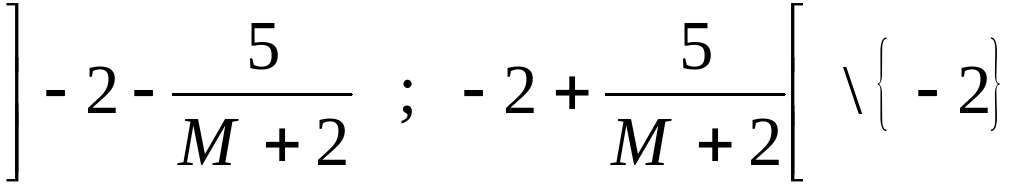3 . Limite finito all’infinito

Data la funzione f(x) : D_f → C_f , con D_f R , C_f R e D_f illimitato, si definisce limite finito per x che tende all’infinito, il numero reale l che soddisfa alla seguente condizione:

l è limite della funzione f(x) per x che tende a + - ), e si scrive

( ), se , tale che , ( ).

N.B.: in questa definizione è interessante considerare ε ‘piccolo a piacere’, cioè ε → 0.

Questo tipo di limite implica l’esistenza di asintoto orizzontale di equazione

Esempi

Verificare l’esistenza di un limite secondo la definizione, significa risolvere la disequazione indicata, in questo caso , e trovare come risultato un sottoinsieme illimitato di D_f.

3.a Data la funzione , verifica che .

D_f = R ;

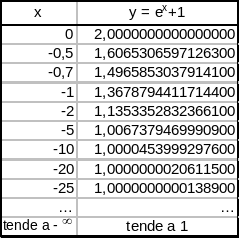
Verifica empirica:

Verifica secondo la definizione:

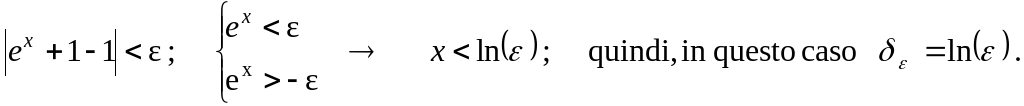
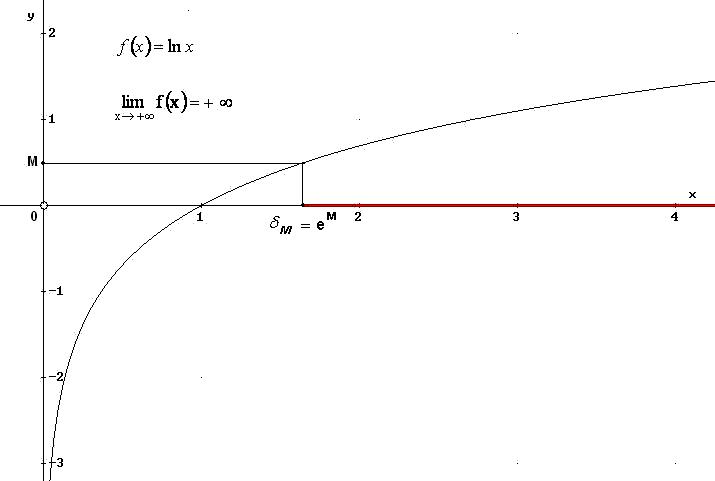
Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, la soluzione è un sottoinsieme illimitato di D_f : ]-  ; ln(ε) [.

La funzione ammette asintoto orizzontale di equazione y = 1.

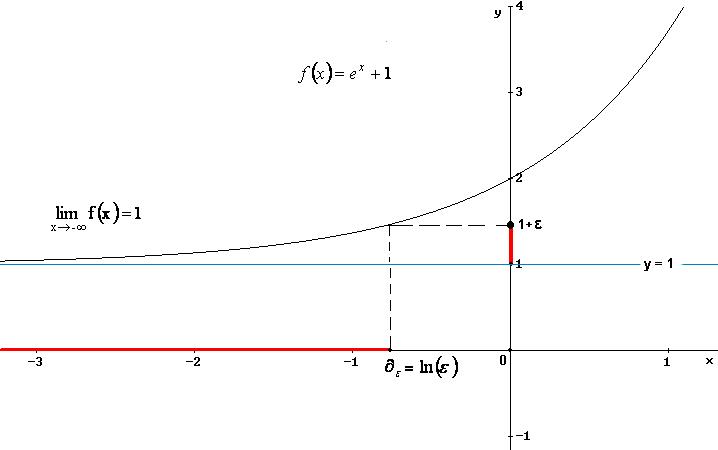
3.b Data la funzione , verifica che .

Il limite indicato è stato verificato, perché, risolvendo la disequazione della definizione, la soluzione è un sottoinsieme illimitato di D_f :

.

La funzione ammette asintoto orizzontale di equazione y = 2.

4 . Limite infinito all’infinito

Data la funzione f(x) : D_f → C_f , con D_f R , C_f R e D_f illimitato, si dice che il limite della funzione f(x), per x che tende a più infinito (meno infinito), è infinito, e si scrive ( ),

se , tale che ( ).

N.B.: a) in questa definizione è interessante considerare M ‘grande a piacere’, cioè M → +  .

b) in particolare, se il limite è + -  ), basta che sia verificata la disequazione f(x) > M
( f(x) < - M ) .

Esempi

Verificare l’esistenza di un limite secondo la definizione, significa risolvere la disequazione indicata, in questo caso , e trovare come risultato un sottoinsieme illimitato di D_f.

4.a Data la funzione , verifica che .

D_f = R ;

Verifica secondo la definizione:

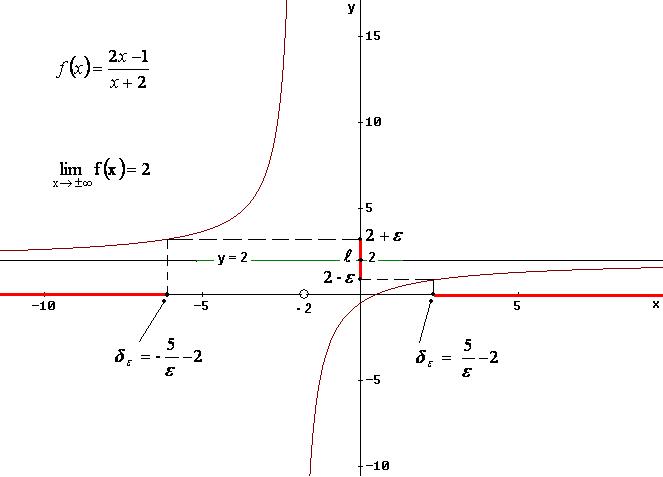
Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un sottoinsieme illimitato di D_f :

.

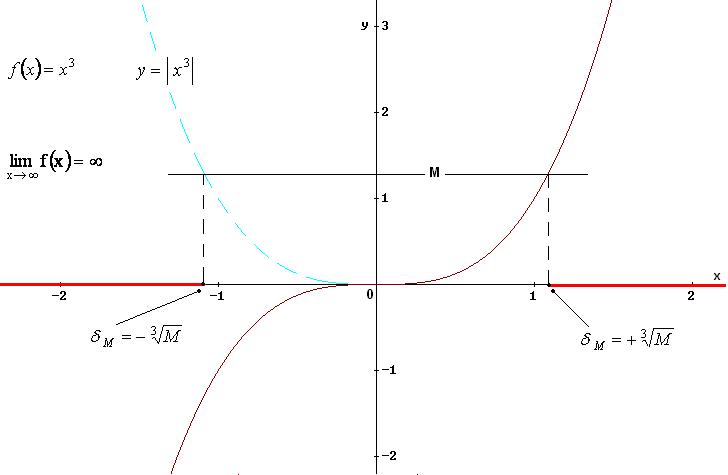
4.b Data la funzione , verifica che .

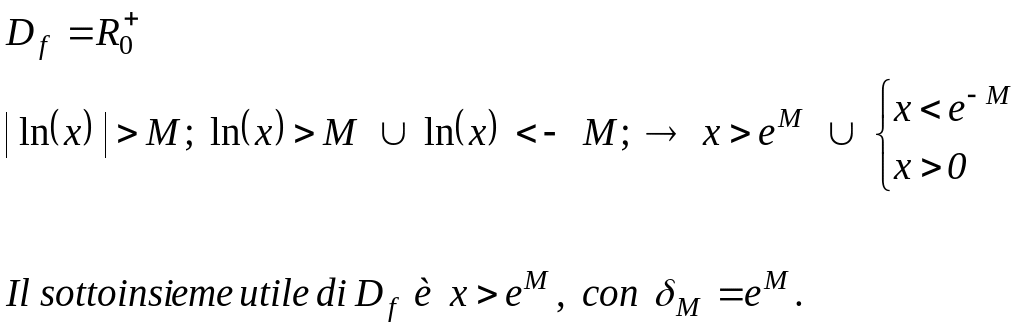
Osservazione:

vista la natura del limite si può procedere in modo più sintetico:

5 . LIMITI DA SINISTRA E DA DESTRA

Per i limiti, finiti o infiniti, in un punto si definiscono i limiti da sinistra e da destra rispetto x₀ .

1. Limite finito in un punto da sinistra e da destra

Data la funzione f(x) : D_f → C_f , con D_f  R e C_f R, considerato il punto x_{0 ,} con x₀ punto d’accumulazione di D_f , si definisce limite finito in x₀ da sinistra (da destra) il numero reale l che soddisfa alla seguente condizione:

l è limite della funzione f(x) per x che tende ad x₀ da sinistra (da destra), e si scrive , se , tale che , .

Esempio

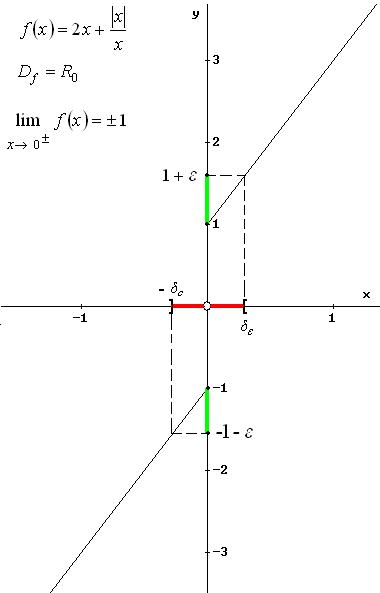
5.1 Data la funzione , verifica che .

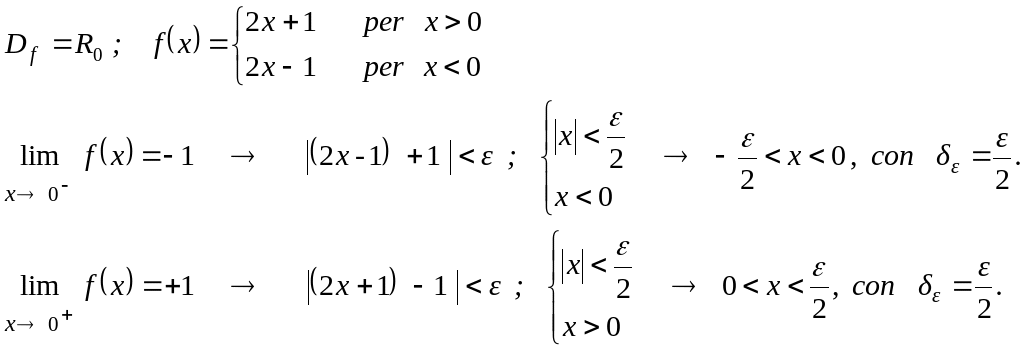
2. Limite infinito in un punto da sinistra e da destra

Data la funzione f(x) : D_f → C_f , con D_f R e C_f R, considerato il punto x_{0 ,} con x₀ punto d’accumulazione di D_f , si dice che il limite della funzione f(x), per x che tende ad x₀ a sinistra (da destra), è infinito, e si scrive

,

se , tale che .

Esempio

5.2 Data la funzione ( vedi esempio 2.a), verifica che .

Nell’esempio 2.a abbiamo considerato il limite all’infinito in ‘valore assoluto’
(), in questo contesto lo consideriamo in senso relativo (  ).

D_f = R \ {0} .

N ota bene1°

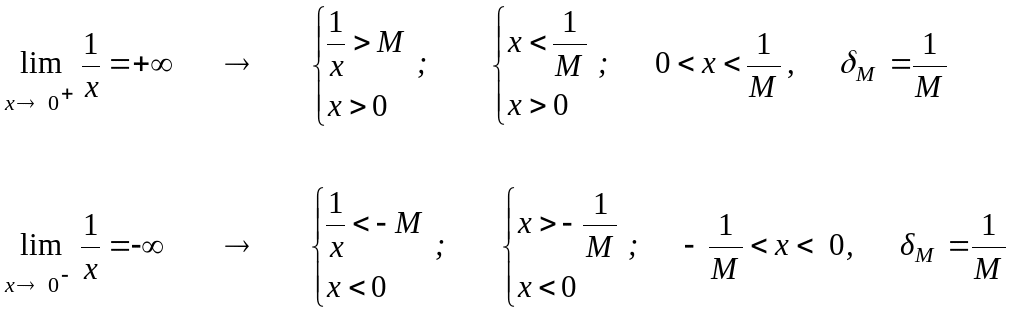
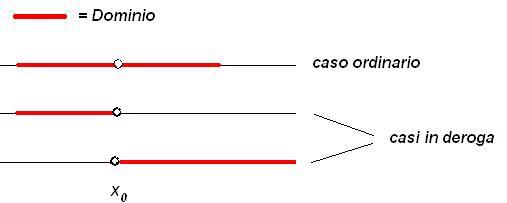
Una funzione ammette limite in un punto soltanto quando in questo punto esiste il limite da destra e da sinistra della funzione e questi due limiti sono uguali (in ‘valore assoluto’ per il limite infinito); il valore comune dei due limiti è il valore del limite della funzione in quel punto:

In deroga a questa regola, si può affermare che una funzione ammette limite in senso assoluto in un punto x₀, anche quando questo limite coincide solamente o con limite sinistro o con il limite destro, se a destra o a sinistra di x₀ la f(x) non è definita.

Esempi:

- Dall’ esempio 5.1, osservo che, data la funzione , con
, in x₀ = 0 esistono i limiti da destra e da sinistra, ma essendo
diversi, non esiste il limite in senso assoluto.

- Dall’ esempio 5.2, osservo che, data la funzione , con ,
in x₀ = 0 esistono i limiti da destra e da sinistra, sono uguali (  in ‘valore assoluto’),
quindi esiste il limite in senso assoluto e vale  .

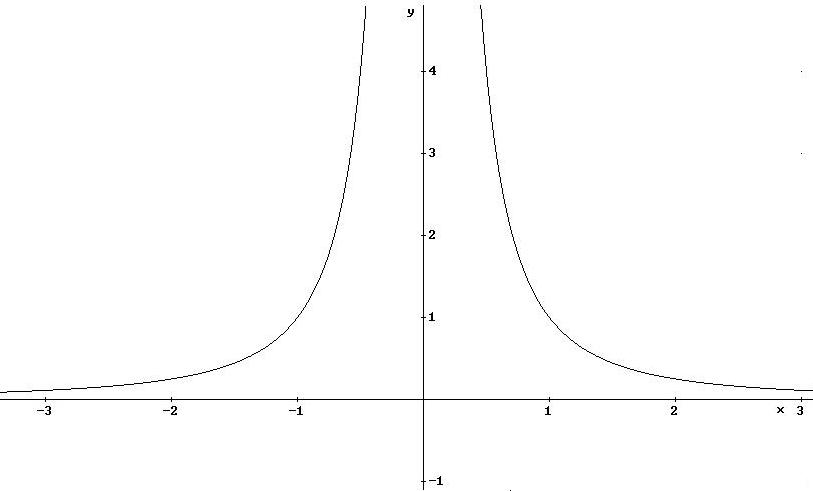
- Dall’ esempio 6.1, osservo che, data la funzione

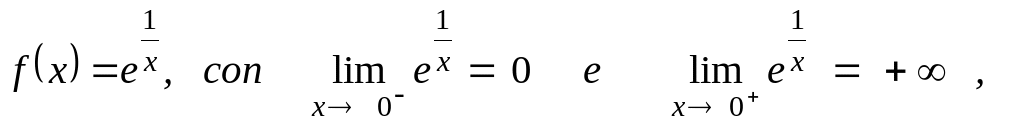
in x₀ = 0 esistono i limiti da destra e da sinistra, ma essendo diversi, non esiste il
limite in senso assoluto.

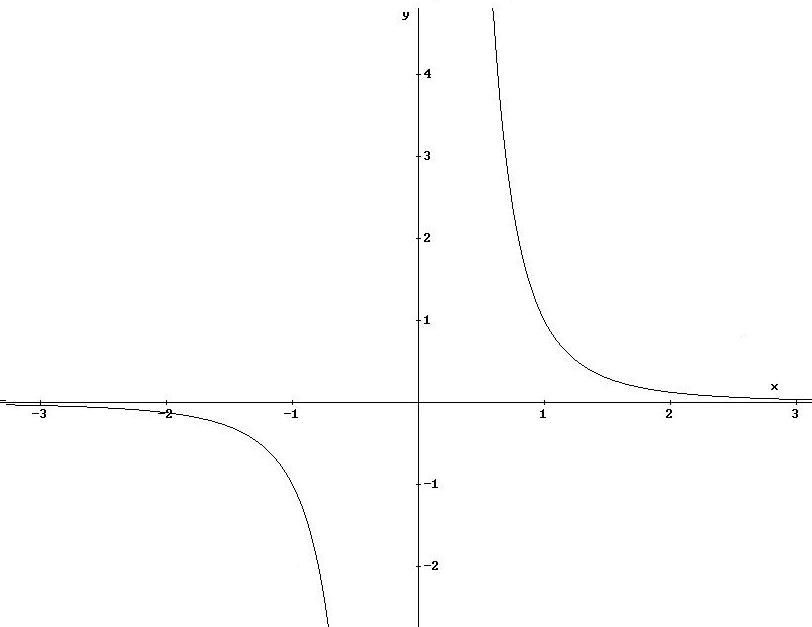
- Dall’ esempio 6.2, osservo che, data la funzione

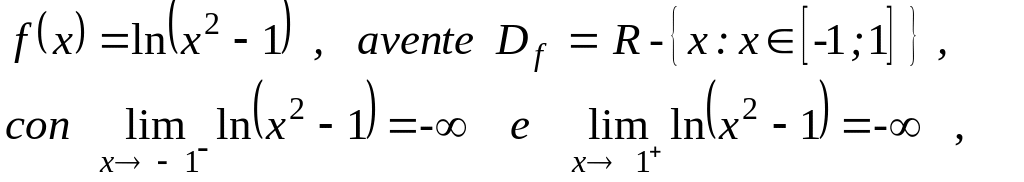
in x₀ = -1 esiste solamente il limite sinistro, mentre in x₀ = +1 esiste solamente il
limite destro, tuttavia, considerando il D_f , si può affermare che la funzione in
entrambi i punti ammette limite in senso assoluto.

6 . ESEMPI DI RIEPILOGO

6.1 Data la funzione f(x) = e^1/x , verifica i seguenti limiti:

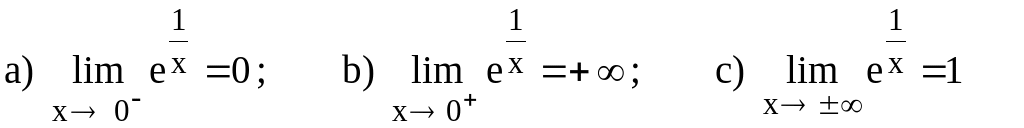
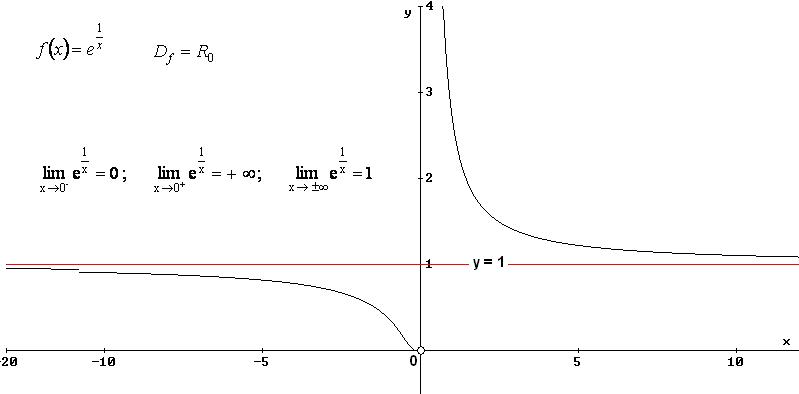
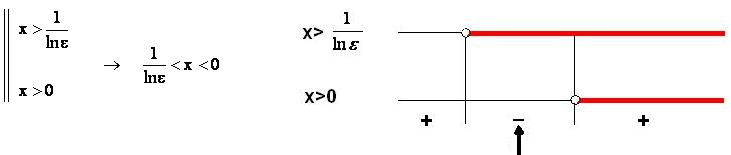
Il limite indicato (limite finito in un punto da sinistra) è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di sinistra di x₀ = 0, privato di x₀ = 0: ; in questo caso .

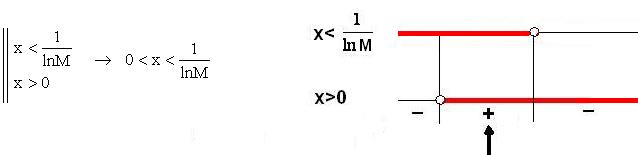
Il limite indicato (limite infinito in un punto da destra) è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di destra di x₀ = 0, privato di x₀ = 0: ; in questo caso .

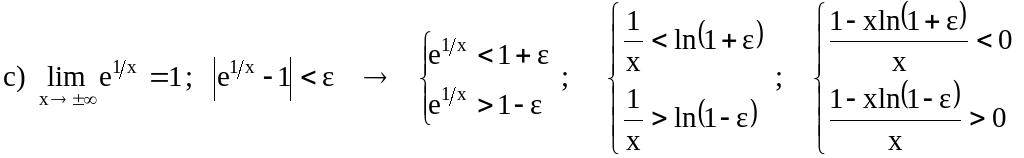
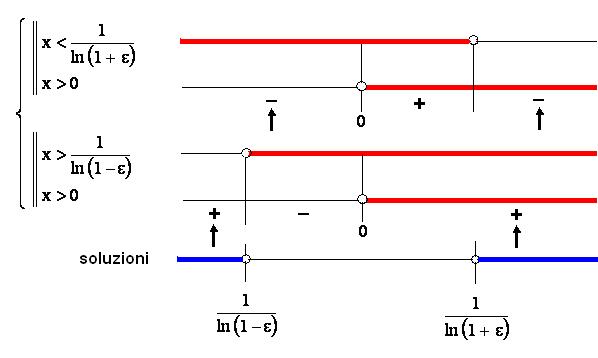
Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, la soluzione è un sottoinsieme illimitato di D_f : .

La funzione ammette asintoto orizzontale di equazione y = 1.

6.2 Data la funzione f(x) = ln(x² -1), verifica i seguenti limiti:

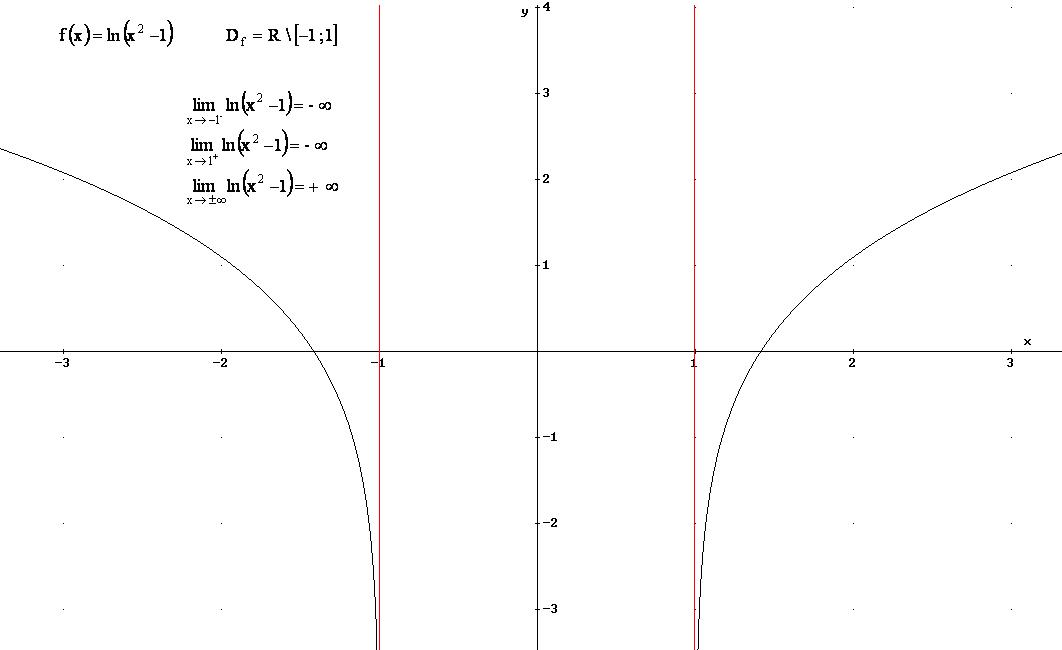
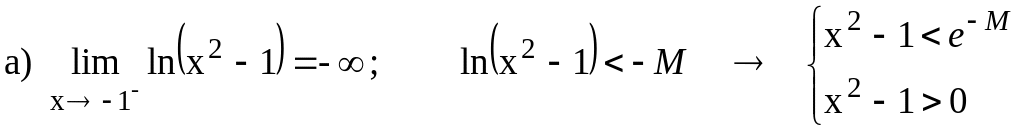
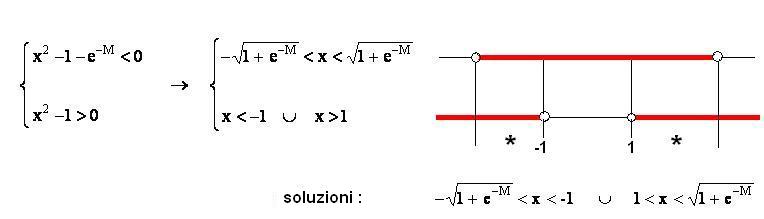
Il limite indicato (limite infinito in un punto da sinistra) è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di sinistra di x₀ = -1, privato di x₀ = -1: ;

in questo caso .

La funzione ammette asintoto verticale di equazione x = - 1.

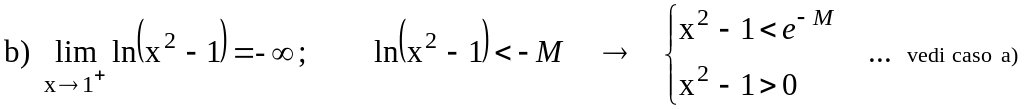
Il limite indicato (limite infinito in un punto da destra) è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di destra di x₀ = 1, privato di x₀ = 1: ;

anche in questo caso ( osserva che la funzione è pari ).

La funzione ammette asintoto verticale di equazione x = 1.

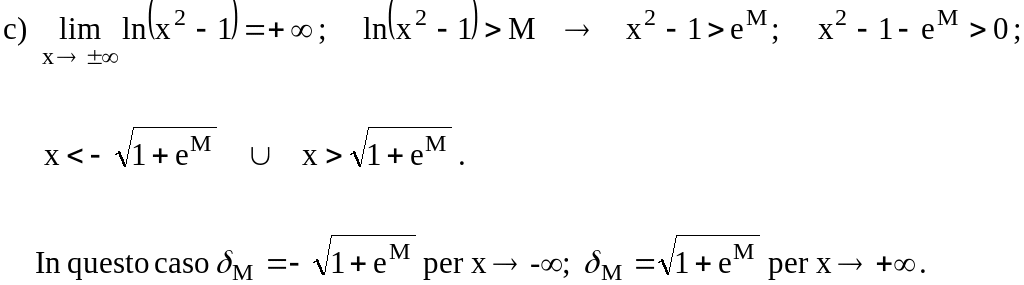
6.3 Data la funzione , con k  R (funzione costante), verifica che

.

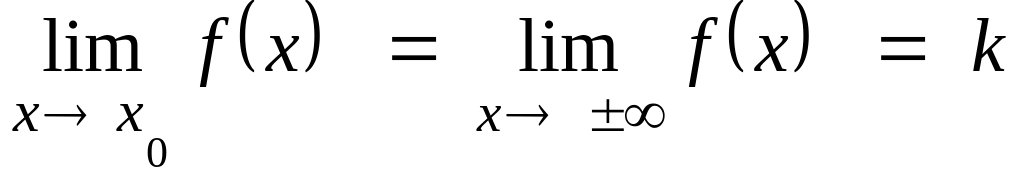La verifica è immediata:

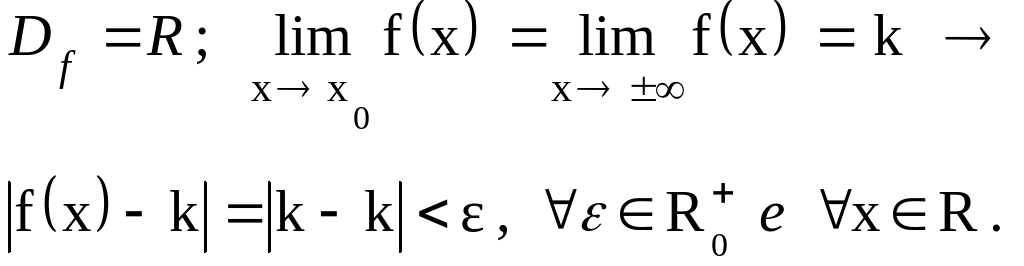
In generale si può quindi dire che ‘ il limite di una costante è la costante stessa ’ .

Osservo che  x  D_f = R la funzione è definita, ammette limite e tale limite coincide con il valore della funzione: ( funzione continua in x₀ )

6.4 Verifica che : .

a) f(x) = sgn(x), D_f = R ;

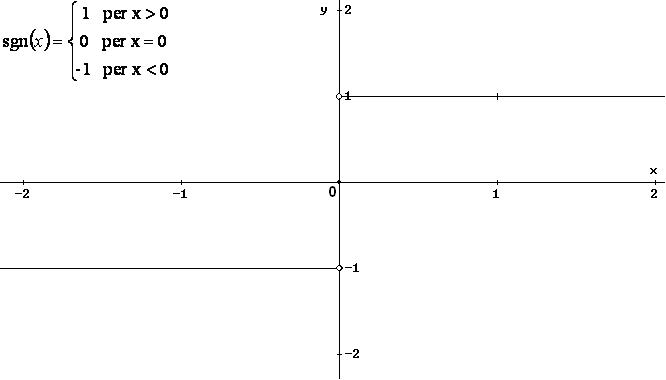
Osservo che nel punto x₀ = 0 la funzione è definita, ma non ammette limite:

b) , D_f = R₀ ; i limiti si verificano come in a) ; il grafico è
identico al precedente, tranne per x = 0, dove la funzione non è definita.

Osservo che nel punto x₀ = 0 la funzione non è definita e non ammette limite:

6.5 Verifica che

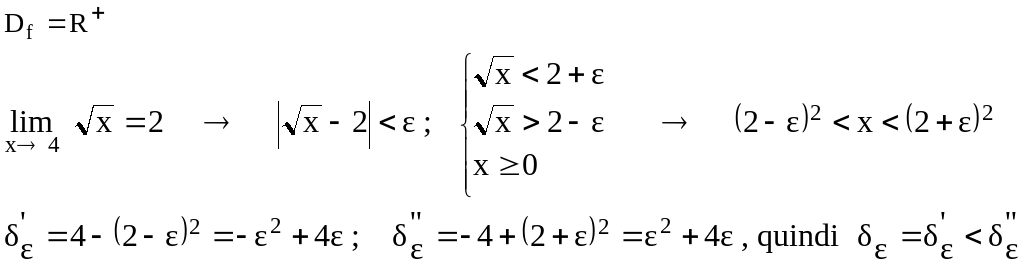
Si può concludere, in modo più raffinato, che , e che l’intorno di x₀ = 4, privato di x₀ = 4, è .

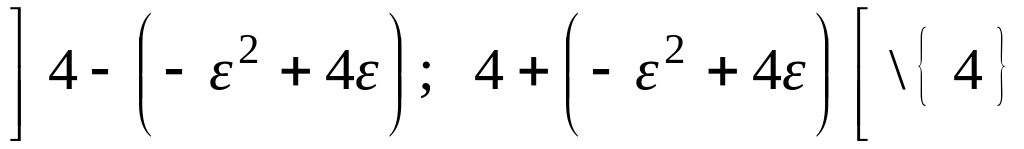Osservo che nel punto x₀ = 4 la funzione è definita, ammette limite e tale limite coincide con il valore della funzione: ( funzione continua in x₀ = 4 )

6.6 Data la funzione 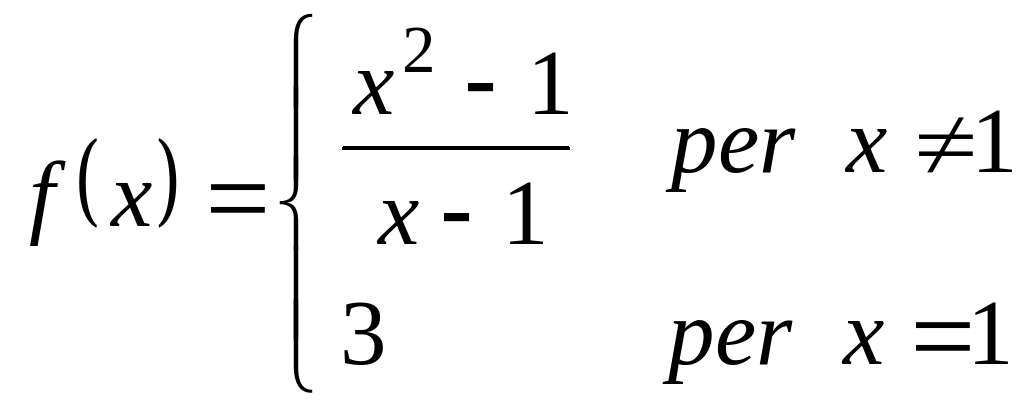, verifica che .

D_f = R ; la verifica del limite è nell’esempio 1.a .

Osservo che nel punto x₀ = 1 la funzione è definita, ammette limite e tale limite non coincide con il valore della funzione: .

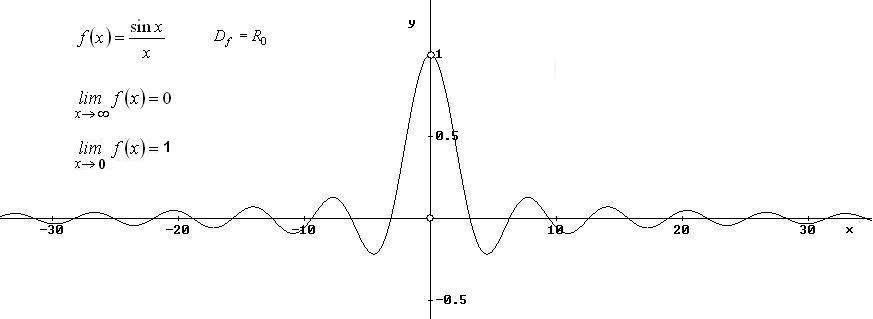
6.7 Data la funzione , verifica che .

Il limite indicato è stato verificato perché, risolvendo la disequazione della definizione, la soluzione è un sottoinsieme illimitato di D_f :

.

La funzione ammette asintoto orizzontale di equazione y = 0.

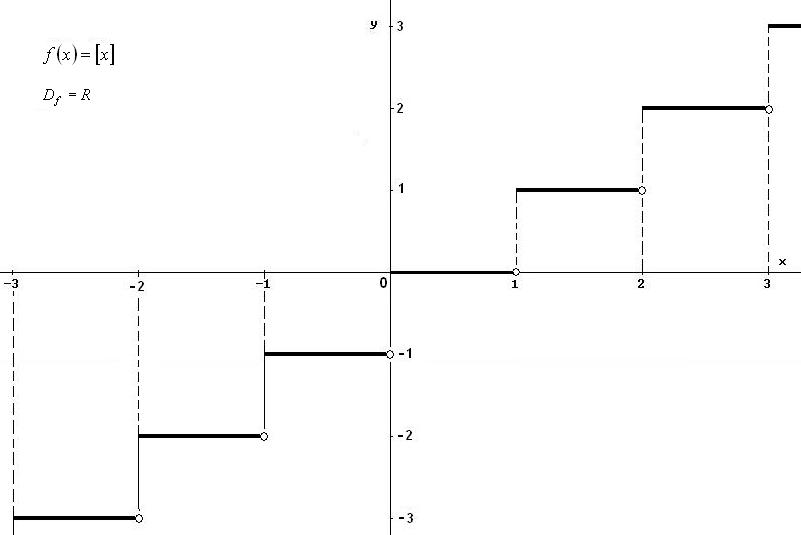
6.8 Data la funzione ‘ parte intera ’ , verifica che .

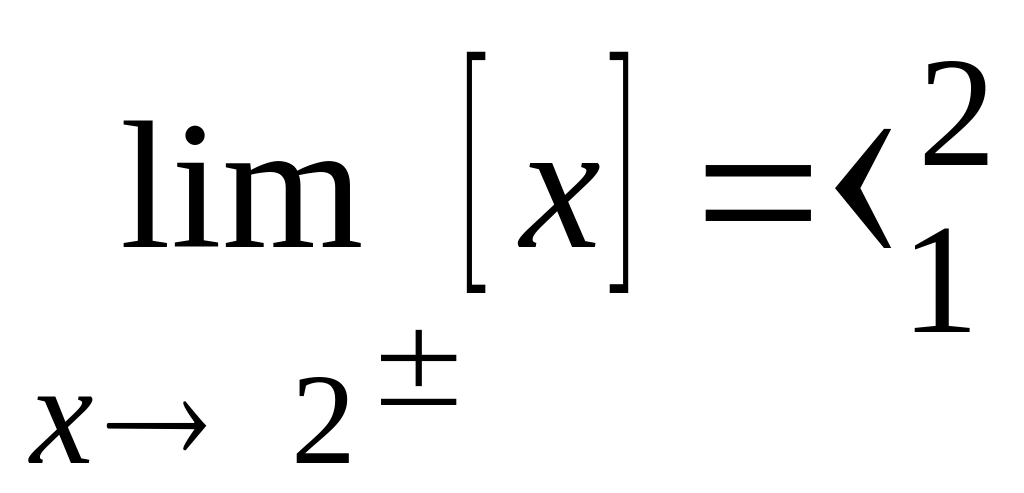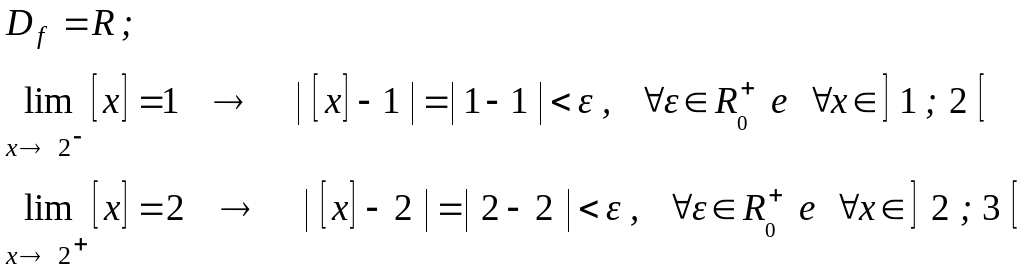
Osservo che nel punto x₀ = 2 ( e così in tutti i punti x  Z ) la funzione è definita, ma non ammette limite:

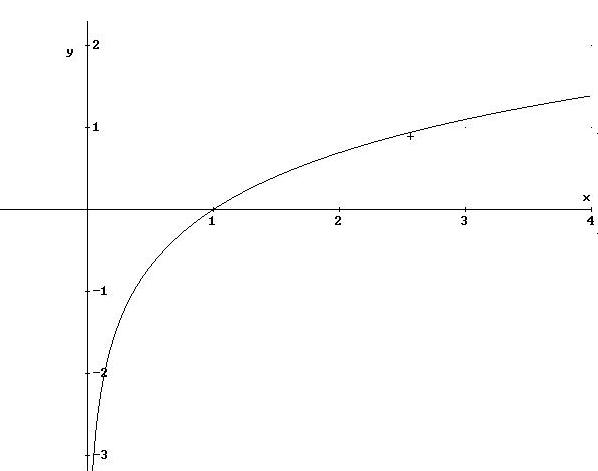
6.9 Data la funzione , verifica che .

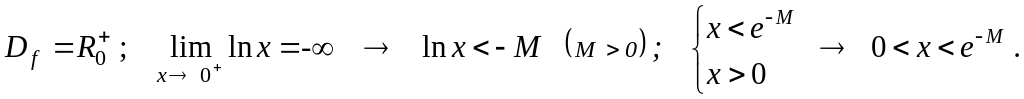
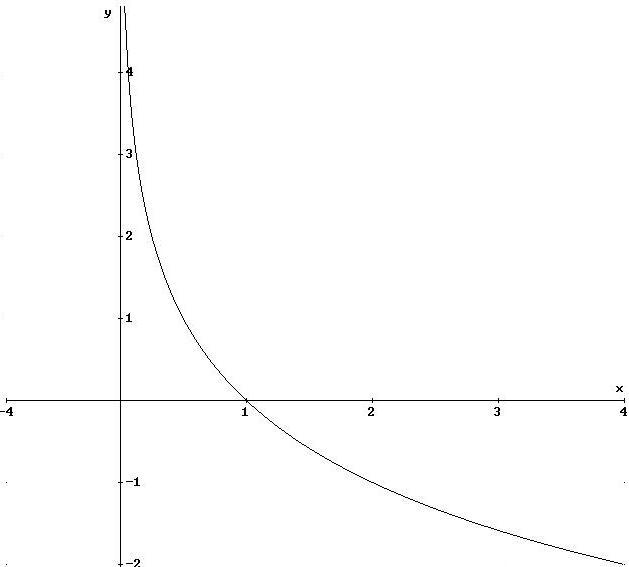
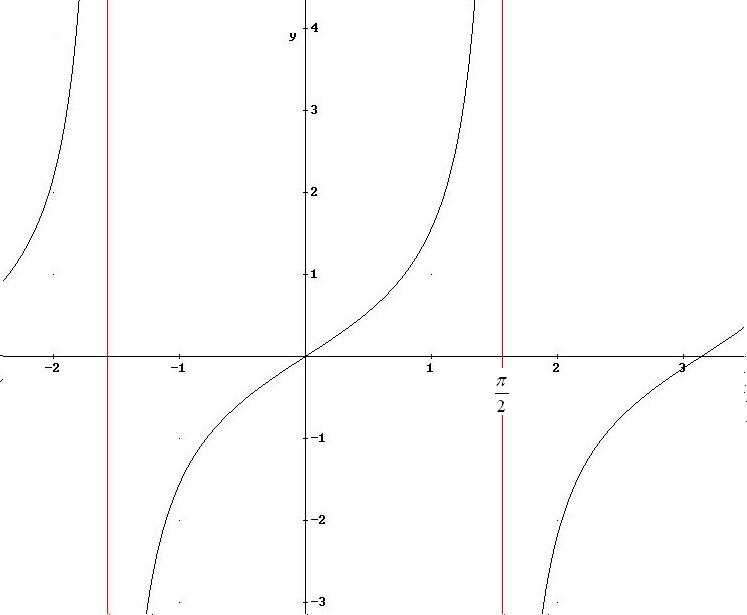
6.10 Data la funzione , verifica che .

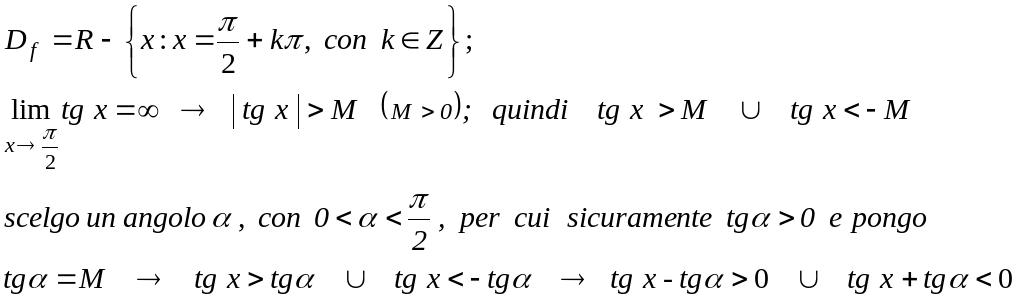
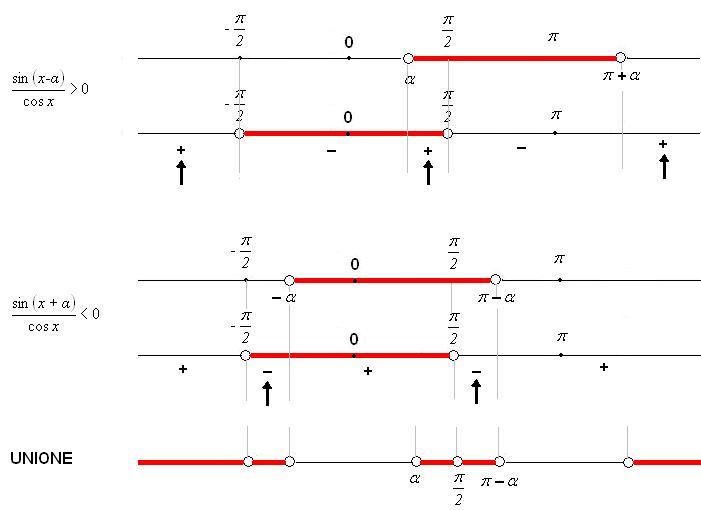Il limite indicato (limite infinito in un punto) è stato verificato perché, risolvendo la disequazione della definizione, ho trovato come soluzione un intorno di x₀ = π/2, privato di x₀ = π/2 : ; questo intorno è tanto più piccolo quanto più α tende a π/2, cioè quanto più M è grande.

La funzione ammette asintoto verticale di equazione x = π/2 .

6.11 Non esistono i seguenti limiti:

,

infatti, poiché sono funzioni periodiche, non si può determinare alcuno dei sottoinsiemi dei D_f che soddisfano alle disequazioni delle definizioni di limite ‘finito all’infinito’ e ‘infinito all’infinito’.

6.12 Data la funzione , con D_f = R₀ , considera i seguenti limiti:

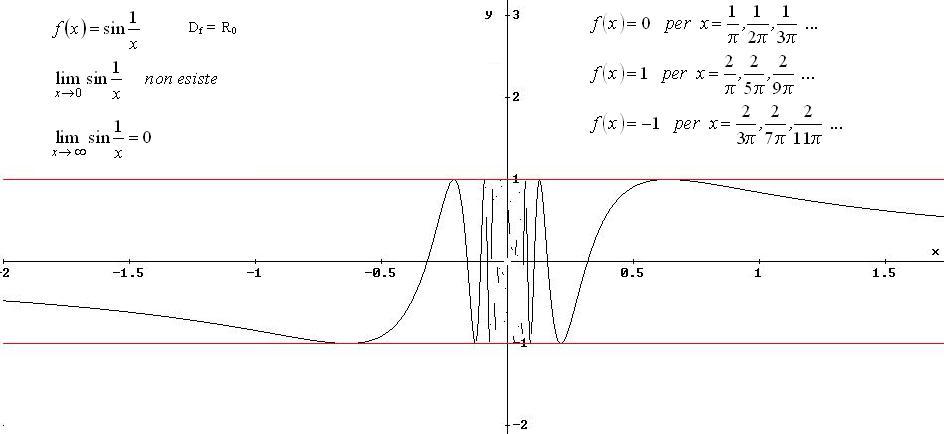
a) Il limite non esiste, perché in un qualsiasi intorno del punto x₀ = 0 , la funzione
compie infinite oscillazioni, tutte di ampiezza uguale a 2, che vanno
restringendosi al tendere di x a zero: non è applicabile alcuna definizione di
‘limite in un punto’.

b) Basta osservare che se x  0, allora 1/x  , quindi posto α = 1/x, si ha:

La funzione ammette asintoto orizzontale di equazione y = 0 .

6.13 Data la funzione , verifica che

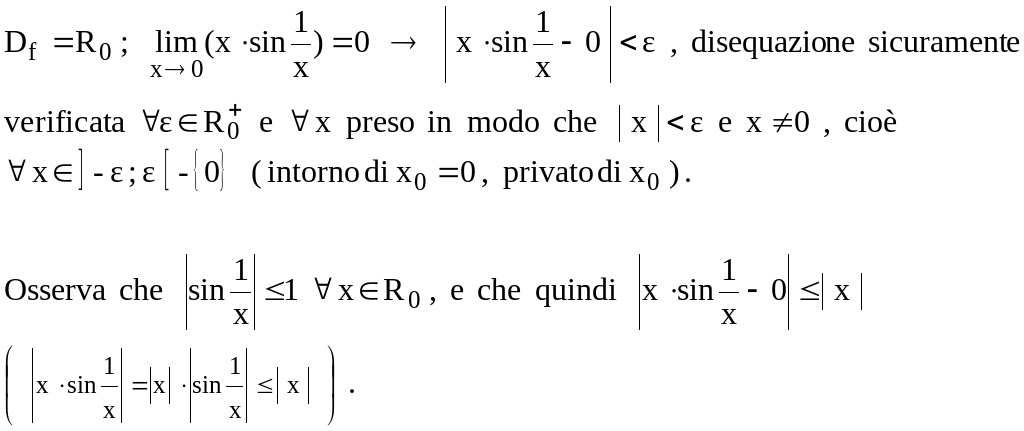
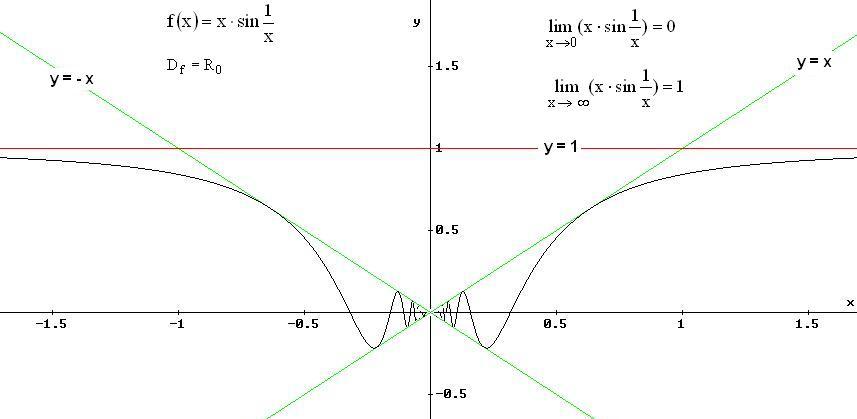
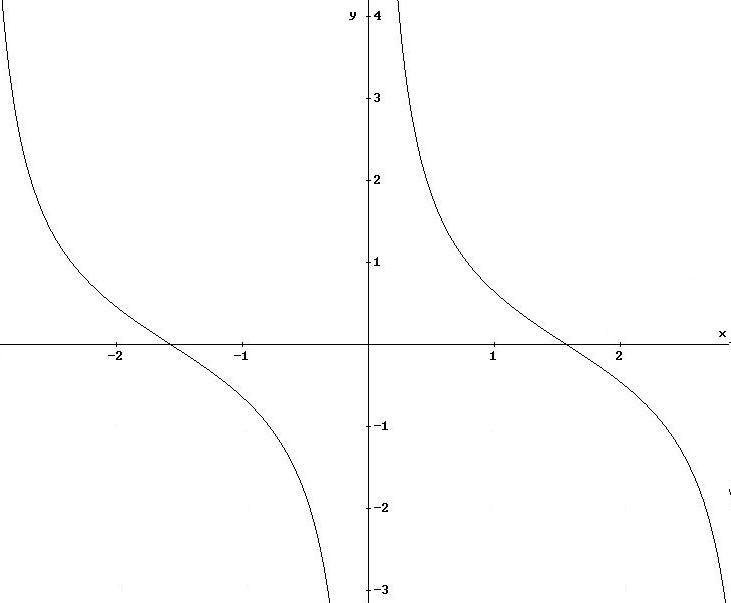
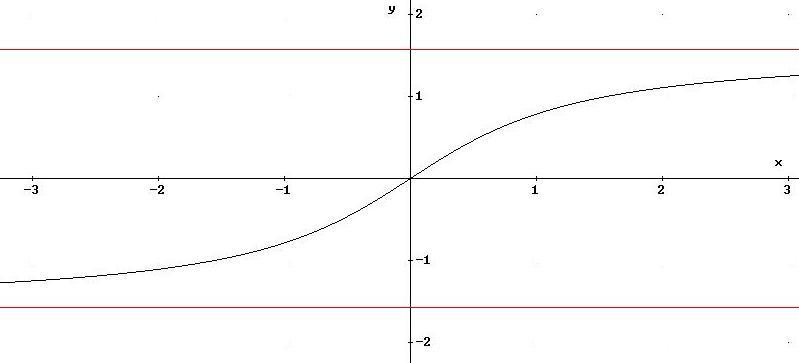
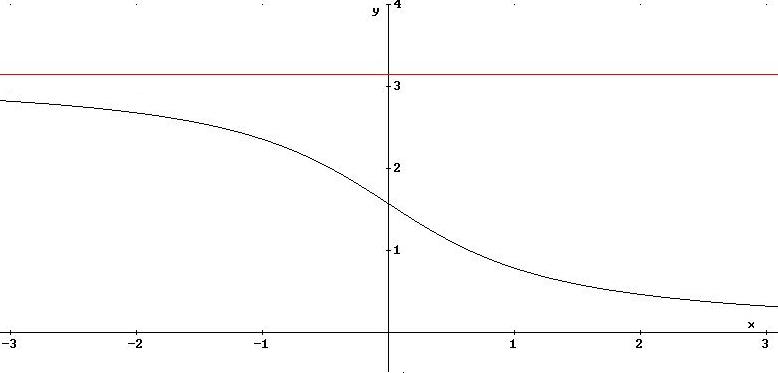
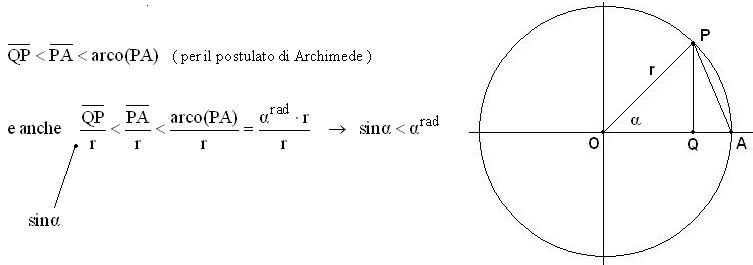
6.14 Data la funzione , verifica che ,  x₀  R .

------------------- N. B. ---------------------

S i possono verificare i limiti analoghi, anche per le altre funzioni goniometriche,  x₀  D_f , cioè in generale:

------------------------------------------

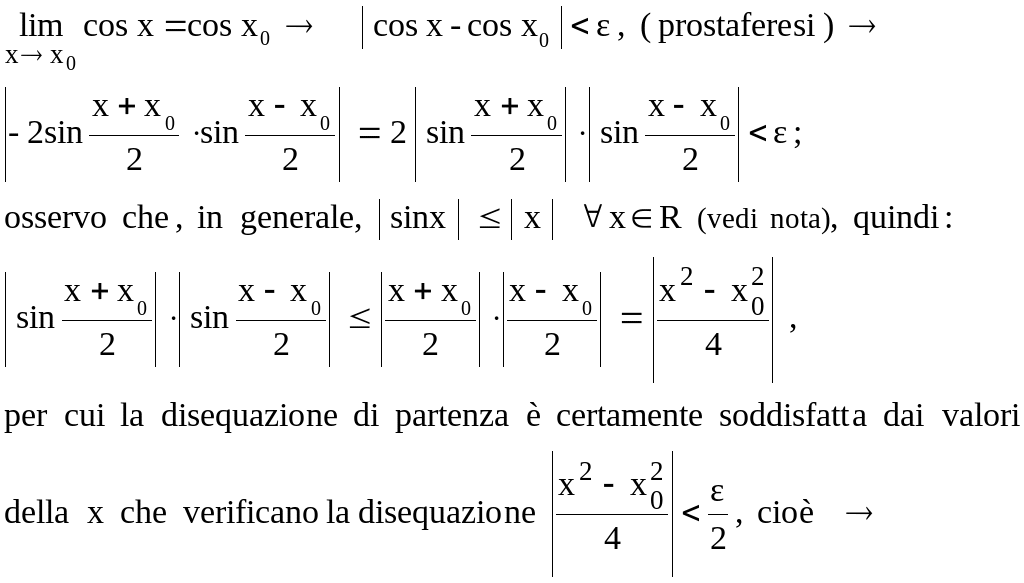
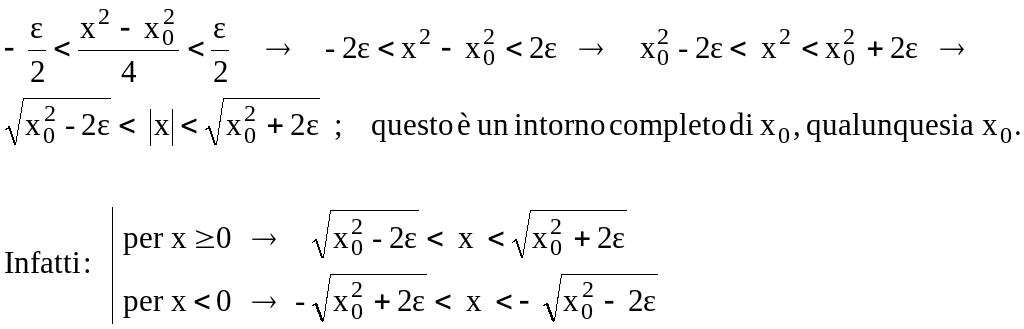
------------------- N. B. ---------------------

- -----------------------------------------

N ota bene 2°

Dagli esempi si osserva che, data una funzione f(x) avente dominio D_f e considerato un punto x₀, punto d’accumulazione di D_f, il comportamento della f(x) al tendere di x a x₀ può presentare i seguenti casi:

nel punto x₀

1. la f(x) è definita, esiste il limite e tale limite coincide con f(x₀) ( funzione continua in x₀ ) ; vedi es.: 6.3 – 6.5 – 6.14

2. la f(x) è definita, esiste il limite e tale limite non coincide con f(x₀); vedi es.: 6.6

3. la f(x) è definita e non esiste il limite; vedi es.: 6.4(a) – 6.8

4. la f(x) non è definita ed esiste il limite; vedi es.: 1.a – 2.a – 6.2(a,b) – 6.9 – 6.10 – 6.13

5. la f(x) non è definita e non esiste limite; vedi es.: 6.1(a,b) – 5.1. – 6.4(b) – 6.12(a)

7 . Limite per eccesso e per difetto

Definizione di limite per eccesso (difetto): diciamo che f(x) tende a l per eccesso (difetto), e si scrive

Esempi:

Vedi esempio 3.b :

Vedi esempio 3.a :

Vedi esempio 6.1 :

8 . Limiti fondamentali

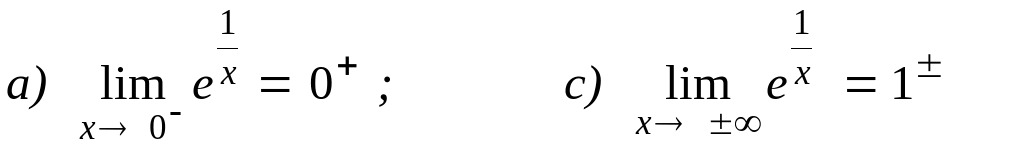
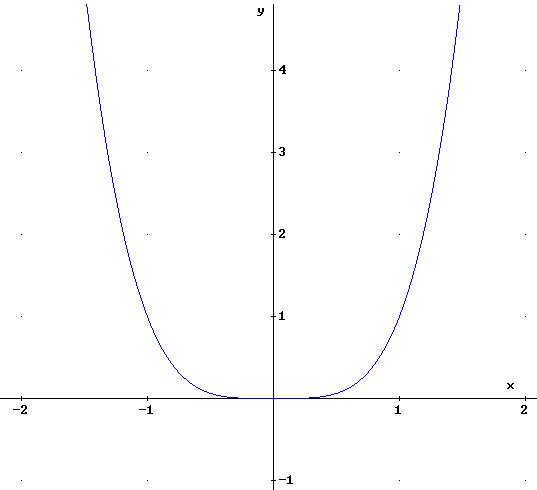
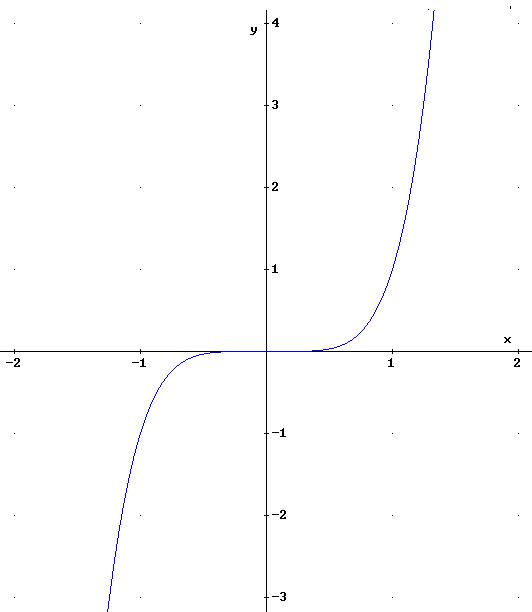
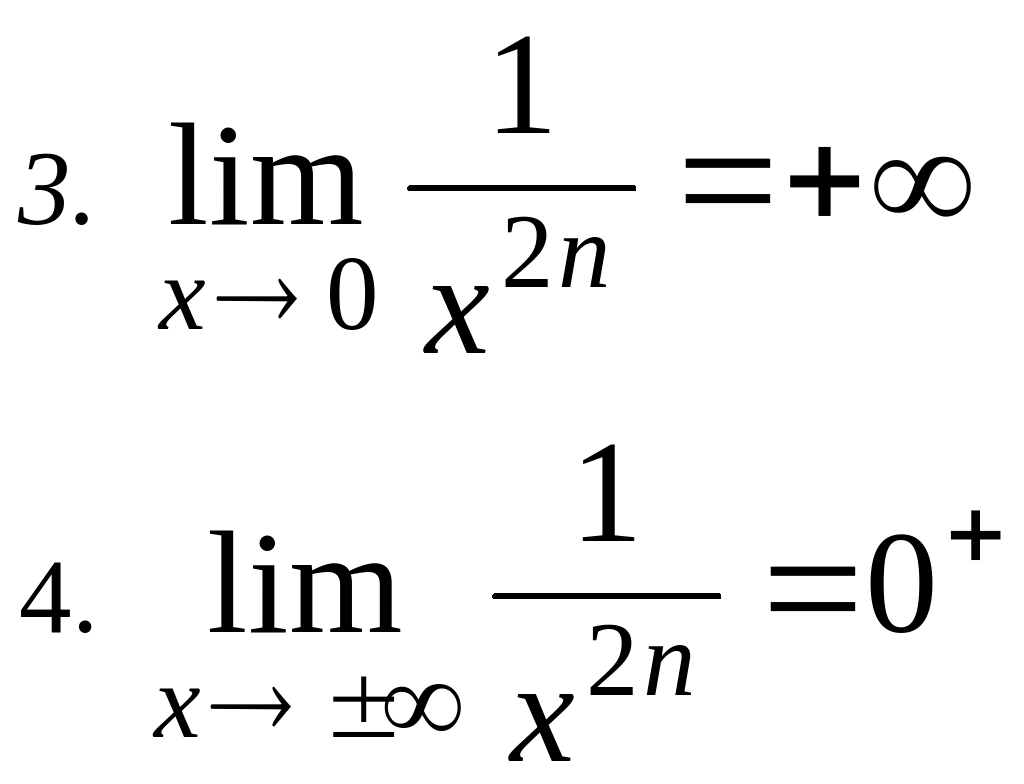
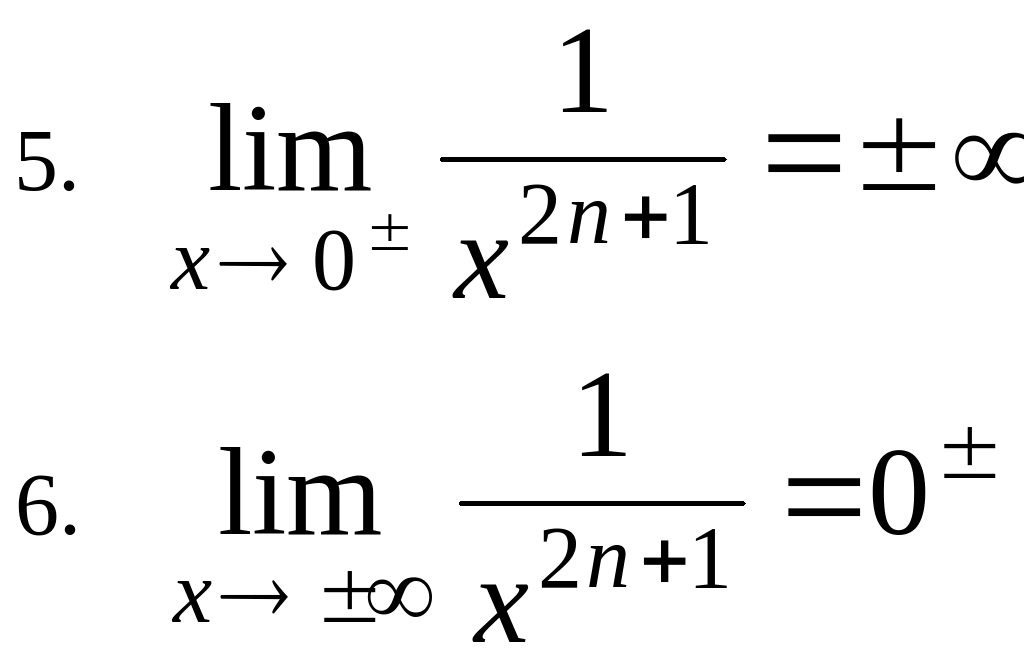
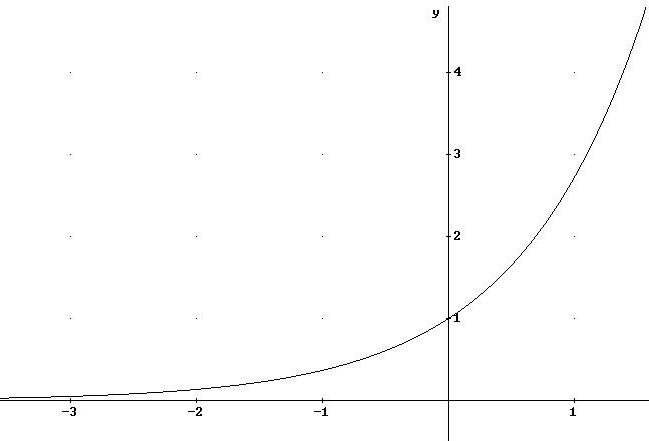
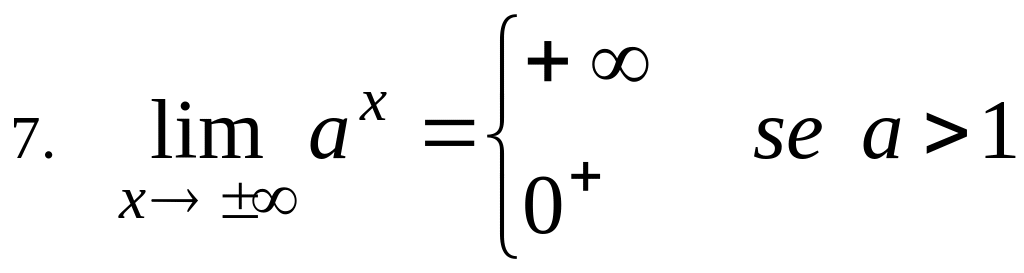
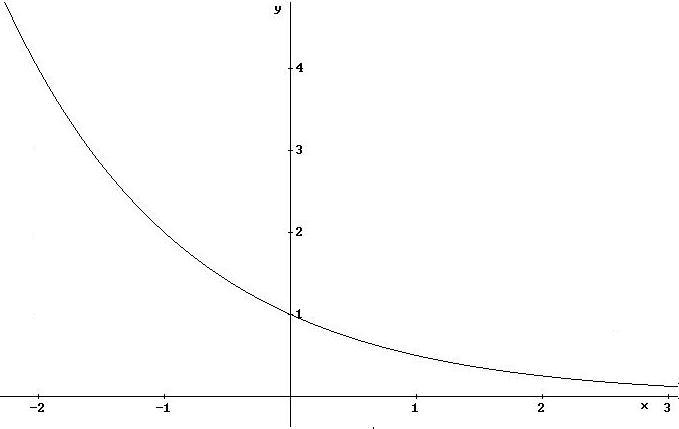
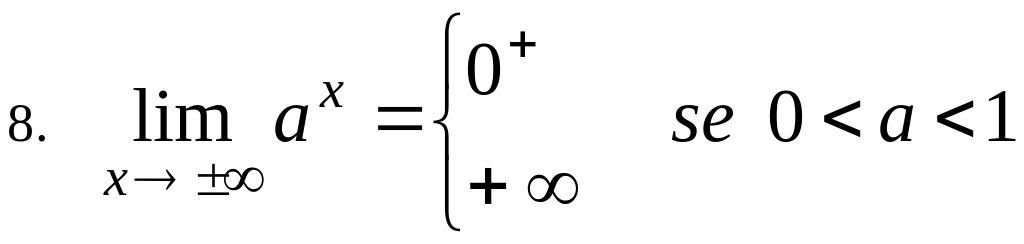
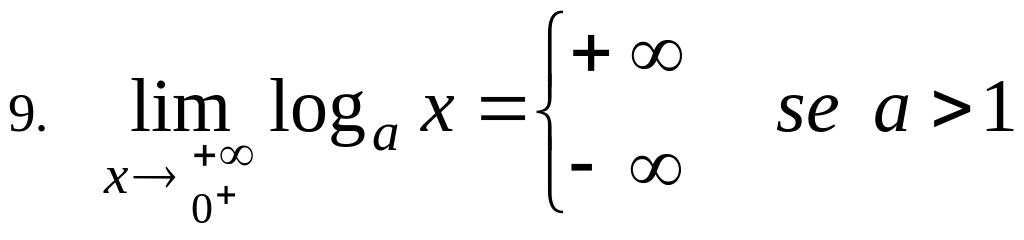
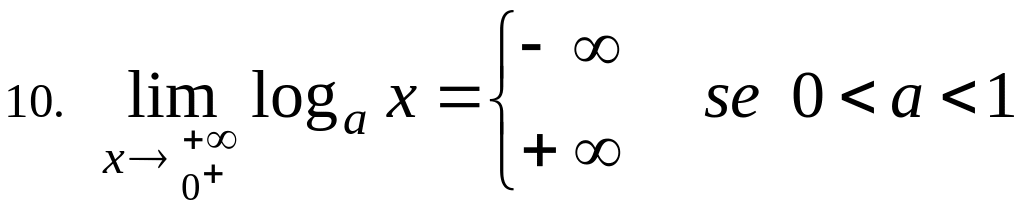
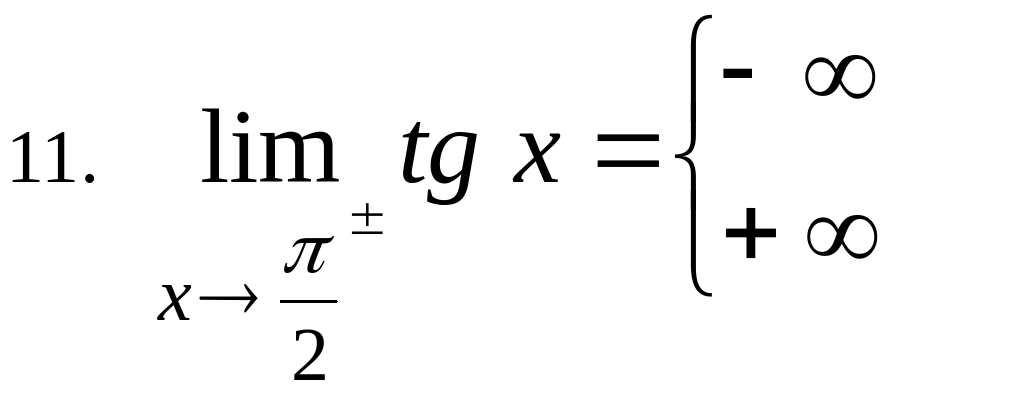
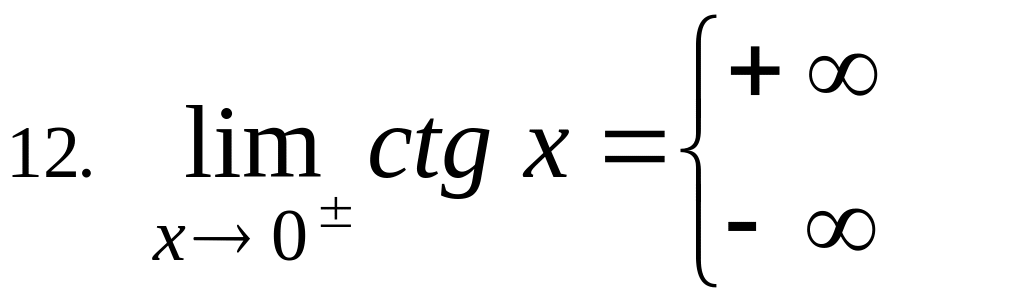
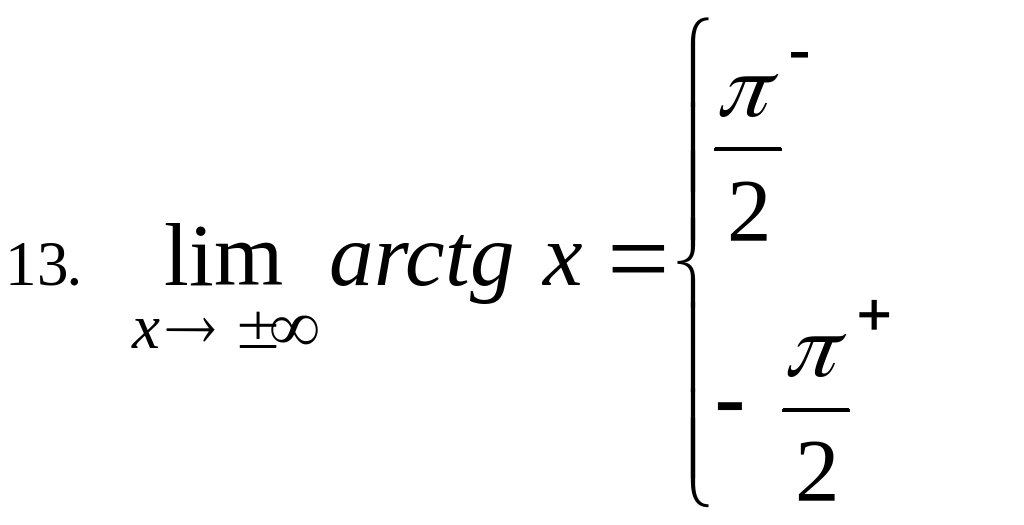
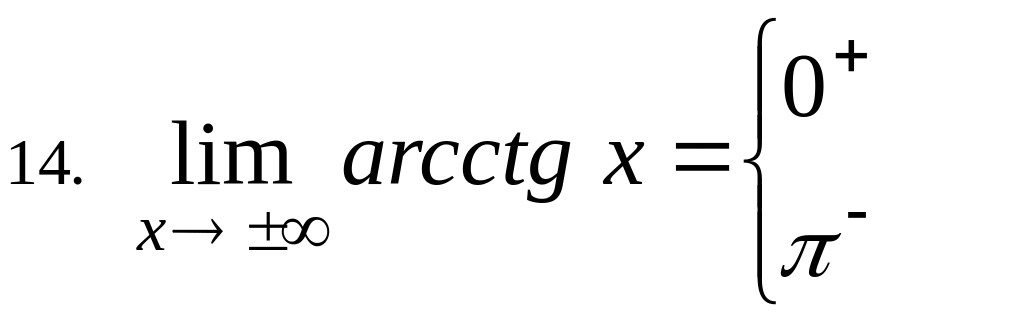
Tags: finito in, (limite finito, punto, finito, limite, limiti

---

• LEY 261991 DE 21 DE NOVIEMBRE DE CONTRATOS CELEBRADOS
• ZNAK SPRAWY AEZS0732016 PAKIET 9 ZMIENIONY ZAŁĄCZNIK NR 29
• FORMULARIO DE SOLICITUD DE RENOVACION DE SISTEMA EXCEPCIONAL DE
• HEAD OF MARKETING ZSL COMMERCIAL EVENTS MANAGER LONDON ZOO
• “2010 AÑO DEL BICENTENARIO DE LA REVOLUCIÓN DE MAYO”
• TRANSCRIPCIÓN DE LA ENTREVISTA REALIZADA A JAUME RAURICH CANEMASES
• MEIOSIS FORMS THE MOST SIGNIFICANT PART OF PROCESS OF
• HACIA UN TEATRO DE OBJETOS SÍNTESIS DEL ENSAYO EN
• A CRITIQUE OF THE APOTHEOSIS OF HOMER BY INGRES
• MENTORING RELATIONSHIP AGREEMENT WE THE UNDERSIGNED AGREE ON THE
• É P Ü L E T Ü Z E
• MODULE ENHANCEMENT SCHOOL OF LAW FEB 2010 CONSIDER THE
• PRIVATE TEACHERS OF CURRENT PHILHARMONIC ASSOCIATION MUSICIANS NAME PHONE
• LP TYTUŁ STR 1 SŁUPOWE STACJE TRANSFORMATOROWE
• STATEMENT OF PRINCIPLES CONCERNING BRONCHIOLITIS OBLITERANS ORGANISING PNEUMONIA NO
• SUBMISSION BY THE NATIONAL CENTRE FOR VOCATIONAL EDUCATION
• DDCS 31 25072013 PRÉFET DE LA HAUTEGARONNE DIRECTION DÉPARTEMENTALE
• ROBERT L FARB INSTITUTE OF GOVERNMENT SUMMARIES OF RECENT
• REGULAMIN ZAKŁADOWEGO FUNDUSZU ŚWIADCZEŃ SOCJALNYCH URZĘDU MIASTA OPOLA I
• AGRUPACION VAL DO ULLA VILA DE CRUCES VEDRA BOQUEIXON
• SCHEDA DI ISCRIZIONE IL SOTTOSCRITTO RESIDENTE A
• CERNST2000053 FEBRUARY 2000 DESIGN AND CALCULATION OF AN EARTH
• CHIEF EXECUTIVE OFFICER UNITUS CAPITAL PAGE 7 POSITION SPECIFICATION
• CONDENSADORES DE HID DE TENTA ELECTRIC DE TAIWÁN
• NAME DATE IT’S CATCHING KEY WORDS INFECTIOUS PROCEDURE
• ESPECIALIDAD EXCURSIONISMO REQUISITOS Y RESPUESTAS 1 DISCUTE CON
• SLOVENSKÁ POŠTA A S POSTSERVIS SEKCIA LOGISTIKY BOJNICKÁ 14
• LIBERAL EDUCATION SPRING 2001 VOLUME 87 NUMBER 2
• ANSWERS TO FINAL EXAMS – SHORT COURSES LOCATED AT
• IMPUESTO SOBRE VEHÍCULOS DE TRACCIÓN MECÁNICA (CONSULTA VINCULANTE V094913

• “DIARIO VESICAL” INSTRUCCIONES LA INFORMACIÓN QUE SE PROPORCIONA EN
• UNIVERSIDAD DE EXTREMADURA VICERRECTORADO DE INVESTIGACIÓN PROGRAMA PROPIO DE
• 5 1PIELIKUMS ATKLĀTA PROJEKTU KONKURSA „ATBALSTS JAUNIEŠU CENTRU DARBĪBAS
• 15_Zal_1_Opis_przedmiotu_zamowienia
• THE ENGLISH VOWEL SPACE OF FILIPINO CHILDREN CHRISTINE C
• CHECK LIST OF PATIENTS FOR DISCHARGE KALAFONG HOSPITAL WARD
• ÖZEL GÜVENLİK HİZMETLERİNE DAİR KANUN KANUN NO 5188 KABUL
• A TUDOMÁNYOS KUTATÓI TEVÉKENYSÉG KREDIT ÉRTÉKEI (100 RÉSZVÉTELI
• RESOLUTION A RESOLUTION DECLARING THE OFFICIAL INTENT OF THE
• IMMOBILIZZAZIONI MATERIALI CASI PARTICOLARI ART 102 TUIR IN
• COMMENT ON A ÉCRIT LES NOMBRES DANS LE SOUS
• BAJNOKI MÉRKŐZÉSEK DÍJAI 1) NAGYPÁLYÁS VAGY CSÖKKENTETT PÁLYAMÉRETŰ
• DEPARTAMENTO DE ESTADÍSTICA TUTORIAL PARA GESTION DE PROYECTOS DE
• ROTARY ROTARY INTERNATIONAL | ONE ROTARY CENTER | 1560
• RECURSOS PER AL TREBALL D’ESTIU DELS ALUMNES DE 6È
• INTEIRO TEOR DA DELIBERAÇÃO 49ª SESSÃO ORDINÁRIA DA SEGUNDA
• EXCMO SR CON CARÁCTER EXTRAORDINARIO MOTIVADO POR LA AUSENCIA
• DOMICILIARY EQUIPMENT SERVICE WHEELCHAIR INITIAL SPECIFICATION FORM PLEASE SUBMIT
• LA LIBERTÉ DEXPRESSION DES DÉTENUS 1 TEXTES ET RÉGLEMENTATION
• SCAJ CONFERENCE CALL – 28TH JUNE 2010 ATTENDEES BRYAN