TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

Pensamiento Decolonial Teoría Crítica Desde América Latina Cátedra Florestan
t3 la Teoría Subyacente a los Mapas Conceptuales y



Teoría de la medida

Teoría de la medida

En matemáticas, una medida es una función que asigna un número, e.g., un "tamaño", un "volumen", o una "probabilidad", a los subconjuntos de un Conjunto dado. El concepto es importante para el Análisis matemático y para la Teoría de la probabilidad.

La Teoría de la Medida es la rama del Análisis real que investiga las σ-álgebras, las medidas, funciones medibles e Integrales. Es de importancia en Probabilidad y Estadística.

Véase también Integración de Lebesgue, Medida de Lebesgue

Tabla de contenidos

Definiciones formales

Formalmente, una medida μ es una función definida en una σ-álgebra Σ sobre un conjunto X con valores en el intervalo real extendido [0, ∞], que satisfaga las siguientes dos propiedades:

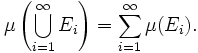
TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

La tripla (X, Σ, μ) se denomina espacio de medida, y los elementos de Σ se denominan conjuntos medibles.

Propiedades

Varias propiedades pueden ser deducidas directamente de la definición.

Monotonía

μ es monótona: si E1 y E2 son dos conjuntos medibles, con E1 ⊆ E2, entonces μ(E1) ≤ μ(E2).

Uniones contables

Si E1, E2, E3, ... es una sucesión contable de conjuntos medibles, su unión será también medible (por la definición de σ-álgebra), y

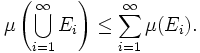
TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

Si se tiene además que En ⊆ En+1 para todo n, entonces

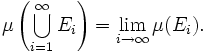
TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

Intersecciones contables

Si E1, E2, E3, ...es una sucesión contable de conjuntos medibles, y En+1 ⊆ En para todo n, entonces la intersección de los conjuntos En es medible (de nuevo, por la definición de σ-álgebra); más aún, si al menos uno de los En tiene medida finita, entonces

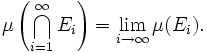
TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

Esta igualdad no es necesariamente cierta si ninguno de los En tiene medida finita; por ejemplo, para cada n ∈ N, tómese

TEORÍA DE LA MEDIDA EN MATEMÁTICAS UNA MEDIDA

Todos estos conjuntos tienen medida infinita, de modo que el límite al lado derecho de la igualdad es ∞; sin embargo, su intersección es vacía y por lo tanto tiene medida 0.

Medidas sigma-finitas

Un espacio de medida (X, Σ, μ) se dice finito si μ(X) es un número real finito (en lugar de ∞). Y se dice σ-finito (leído sigma finito) si X es la unión contable de conjuntos medibles de medida finita. Un conjunto en un espacio de medida tiene medida σ-finita si es una unión contable de conjuntos de medida finita.

Por ejemplo, los números reales con la medida de Lebesgue estándar forman un espacio σ-finito pero no finito. Considérese el intervalo cerrado [k, k+1] para cada entero k; hay una cantidad contable de tales intervalos, cada uno tiene medida 1, y su unión es la recta real completa. Alternativamente, tómense los números reales con la medida de conteo, que asigna a cada conjunto finito de números reales el número de puntos en el conjunto. Este espacio de medida no es σ-finito, ya que cada conjunto de medida finita contiene finitos puntos, y se necesitaría una cantidad no contable de ellos para cubrir la recta entera. Los espacios de medida σ-finita tienen algunas propiedades convenientes; así, la σ-finitud puede ser comparada a la separabilidad de los espacios topológicos.

Completitud

Un conjunto medible S es llamado un conjunto nulo si μ(S) = 0, y conjunto despreciable si está contenido en uno nulo. La medida μ se dice completa si todo conjunto despreciable es medible (y por lo tanto, nulo también).

Una medida puede extenderse a una completa considerando la σ-álgebra de conjuntos T ⊆ X que difieren de un conjunto medible S en un conjunto despreciable; esto es, tal que la diferencia simétrica T Δ S está contenida en un conjunto nulo. En tal caso se define μ(T) = μ(S).

Ejemplos

A continuación se listan algunos ejemplos importantes de medidas.

Otras medidas notables son las de Borel, Jordan, y Radon.

Contraejemplos

Contrariamente a la intuición, no todos los conjuntos son medibles; algunos ejemplos de conjuntos que no tienen medidas o que resultan en paradojas son el conjunto de Vitali, la paradoja de Hausdorff, y la paradoja de Banach-Tarski.

Generalizaciones

Para ciertos propósitos, es útil tener una "medida" cuyos valores no se restrinjan a los reales no negativos y el infinito. Por ejemplo, una función de conjunto contablemente aditiva con valores en los números reales (con signo) se llama medida con signo, mientras que tal tipo de función con valores en los números complejos se llama medida compleja. Una medida que tome valores en un espacio de Banach se llama medida espectral; son usadas a menudo en análisis funcional en el teorema espectral. Para distinguir las medidas usuales, con valores positivos, de las generalizaciones, se habla de medidas positivas.

Otra generalización es la medida finitamente aditiva. Es igual que una medida, salvo que en lugar de requerir aditividad contable, sólo se necesita aditividad finita. Históricamente, esta definición se usó inicialmente, pero no resultó ser tan útil. En general, las medidas finitamente aditivas están conectadas con nociones como los límites de Banach, el dual de L∞, y la compactificación de Stone-Čech. Todas éstas están conectadas de alguna forma con el axioma de elección.

El interesante resultado en geometría integral conocido como teorema de Hadwiger establece que el espacio de funciones de conjunto invariantes por translaciones, finitamente aditivas, no necesariamente no negativas definidas sobre las uniones finitas de conjuntos compactos y convexos en Rn consiste (salvo múltiplos escalares) en una "medida" que es "homogénea de grado k" para cada k = 0, 1, 2, ..., n, y combinaciones lineales de esas "medidas". "Homogénea de grado k" significa que "re-escalar" cualquier conjunto por un factor c > 0 multiplica la "medida" del conjunto por un factor ck. La que es homogénea de grado n es el volumen ordinario n-dimensional. La homogénea de grado n-1 es el "volumen de superficie". La homogénea de grado 1 es una función misteriosa llamada "anchura media" (en inglés, "mean width"), un mal nombre. La homogénea de grado 0 es la característica de Euler.

Obtenido de "http://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_medida"





Tags: medida ===================, la medida, medida, teoría, matemáticas