LESSON 1 VECTORS AND COORDINATE SYSTEMS I POSITION VECTOR
CLASSROOM TESTED LESSON VIDEO DESCRIPTION “SECRETS OF THELESSON PLAN FORMAT FOR ELEMENTARY MIDDLE SCHOOL METHODS
SCIENCE LESSON PLAN IONIC AND COVALENT BODING
Teach Engineering Stem Curriculum Lesson Designing Bridges
UNIT SLAVERY LESSON 25 FREDERICK DOUGLASS (2
013_Spring1_UKS2_Yr5_Lesson_5
Lesson 1: Vectors and Coordinate Systems
Lesson 1: Vectors and Coordinate Systems
I. Position Vector
A. Definition:
Consider an object (a baseball for instance) which is located at some arbitrary point in space (point P). We need to develop a way of describing the location of the ball in terms of mathematics. The method that physicists have developed is called the position vector!!
The position vector for an object is the vector drawn from the origin of a coordinate system to the location of the object.
I
n
the drawing below, the position vector
(shown in green) is drawn from the origin to the location of our
baseball at point P.
P
B. Is the position vector unique?
Since the position vector is defined mathematically in terms of a coordinate system, it is not unique since the coordinate system is not unique. For instance, John might specify the position of the library (green arrow) with a coordinate system’s whose origin is the science building while Susan specifies the position of the library (blue arrow) with respect to the math building.
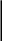
P
Mathematically, these are two different ways of specifying the same physical point in space (the location of the library). Thus, these two mathematical descriptions must be related to each other in some way. Such relationships are known in physics as transformation equations and are very important. In this case, the connection is simply the relationship for adding vectors. The library’s position vector as given by Susan is the sum of John’s position vector according to Susan (shown in red) and the library’s position vector according to John.
You might be inclined to remark that all of this is trivial and even that it is a waist of time. All of this material should be review from your introductory physics course. I encourage you to reject such quick judgments and to reflect deeply upon each concept that we study in this course. The reason that I have chosen to include this material is to remind you of some very important physics and to highlight the course goals. First, you should remember from your introductory physics course that many other physics quantities are derived from the position vector including displacement, velocity, acceleration, linear momentum, angular momentum, etc. Thus, the question of reference frames and transformation equations is extremely important in physics. Secondly, a major reason for the course is not to solve problems involving balls rolling down inclined planes, but to develop an understanding of the way in which physical systems can be represented in mathematics. By learning to apply mathematics to mechanical systems where you have some physical intuition, you build the skills needed for more advanced physics courses (Relativity, Quantum Electrodynamics, etc) where intuition based upon everyday experience will be of little help.
II. Velocity Vector
A. Definition:
The velocity of an object with respect to a coordinate system is defined as the time rate of change of the object’s position vector in that coordinate system.
B. Is the velocity vector unique?
No, the velocity vector is not unique. Observers using two different coordinate systems might disagree on the velocity of an object.
You might be inclined to believe that this is a mathematical artifact and that you could do an experiment to determine if the object is moving or not. However, one of the fundamental principles of physics states that it is impossible to devise an experiment that can actually detect absolute motion. All motion is dependent on the observer.
III. Acceleration Vector
A. Definition:
The acceleration of an object with respect to a coordinate system is defined as the time rate of change of the object’s velocity vector in that coordinate system.
B. Is the acceleration vector unique?
No, the acceleration vector is not unique. Observers using two different coordinate systems might disagree on the acceleration of an object.
IV. Cartesian Coordinate System
You should have been introduced to the Cartesian Coordinate system in your introductory physics course. In this system, an arbitrary point in space such as point P show below is defined by three coordinates (x,y,z).
A. Position Vector
We have already discussed that
a position vector can be written mathematically in more than one way.
In this case, we choose the write the position vector as the sum of
three other vectors (
,
,
and
)
as shown below.
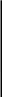
You may remember that a unit
vector is a vector of magnitude (length) 1 with no units that is used
solely to provide direction.To specify the direction of these three
vectors (
,
,
and
),
we define three unit vectors (one for each of our coordinates). These
unit vector are
which points in the +x direction
which points in the +y direction
which points in the +z direction.
By multiplying each unit vector by its associated coordinate, we can produce our three required vectors.
This is just a case of multiplication of a vector by a scalar. If the scalar (coordinate) is positive then the resultant vector points in the same direction as the unit vector. If the scalar (coordinate) is negative then the resultant vector is in the opposite direction (rotated 180 degrees) from the direction of the unit vectors. Putting this into our relationship for the unit vector, we get
Again, you should have already seen this result in your introductory physics course. Did you understand the process by which it came about or did you just memorize it? Often in introductory physics classes, we can take advantage of our students’ every day experiences to teach certain physics principles. Your instructor may have discussed using a combination of North/South and East/West to drive between your house and the grocery store. Because the Earth is relatively flat based upon your everyday experience, most students have an intuitive feel for Cartesian Coordinates. However, we will be working with other coordinate systems so you need to understand actual mathematical process.
B. Velocity Vector
We now use the definition of velocity to develop the relationship for Cartesian coordinates.
The three unit vectors (
,
,
and
)
are constant (remember that for a vector this means constant in
direction as well as constant in magnitude) so their derivatives are
zero!!!
There are several important things that you should take away from this exercise. First, one of the advantages of working with Cartesian coordinates is that the unit vectors don’t enter into the Calculus. In other coordinate systems, you will have to take derivatives of unit vectors!! Secondly, the result shows that the velocity component in each direction depends only on the time rate of change of that coordinate!! Therefore, motion along one axis is independent of motion along either of the other axis. This is why a ball thrown horizontally will hit the Earth at the same time as a ball dropped from the same height provided we neglect the minute curvature of the Earth. It is also why we were able to break rectilinear motion problems into parts in your introductory physics course.
C. Acceleration Vector
We now use the definition of acceleration to develop the relationship for Cartesian coordinates.
Again, we use the fact that
the derivative of our three unit vectors (
,
,
and
)
are zero!!!
Here we see that the acceleration components in each direction are independent.
V. Cylindrical Coordinate System
In this system, an arbitrary point in space such as point P show below is defined by three coordinates (, , and z) as shown below.
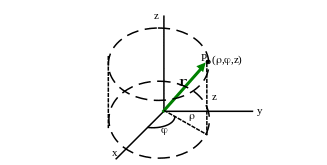
In the drawing, point P is on the surface of an imaginary cylinder of radius , height h, and with the projection of its position vector onto the x-y plane at an angle from the x-axis. You also used this coordinate system in introductory physics to handle rotation problems. However, you probably just memorized the results of the math like the formula for centripetal acceleration instead of actually performing the math operations!!
A. Unit Vectors
Following the procedure for our past work, we are going to define a unit vector for each of the three coordinates. The first unit vector is found by only allowing to vary while keeping and z constant. This amounts to moving along the radius of the cylinder in the direction of an increasing radius. The second unit vector is found by only allowing to vary while keeping and z constant. This amounts to walking counter clockwise around a circle. The third unit vector is found by only allowing z to vary while keeping and constant. This amounts to walking in the +z direction.
points in the + radial direction
points
in the direction of increasing angle
points
in the +z direction.
(,,z) P x y z
Since the unit vectors
and
lie in the x-y plane and do not depend on z, it is often useful to
have the following additional diagram when working out the Calculus:
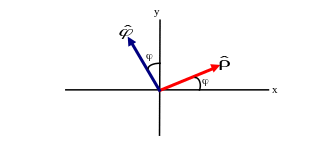
Using our knowledge of the dot product and components, we see that
These are useful relations for doing the Calculus!!
B. Position Vector
In cylindrical coordinates, we can write the position vector in as the sum of only two vectors:
(,,z) P x y z
Thus, we have the position vector in cylindrical coordinates as
You might be surprised that there is no component. This is just one of many places where your intuition from Cartesian coordinates can get you into trouble. Also, you should consider the fact that is an angle and not a distance. Thus, a component in the direction would also have the wrong units unless the term also contained either z or .
C. Velocity Vector
We now use the definition of velocity to develop the relationship for cylindrical coordinates.
The unit vectors (
and
)
are not constant since their direction depends on the location of
point P. Therefore, we will have to take their derivatives!! We do
this by replacing each unit vector with its representation in
Cartesian coordinates and then do the Calculus. Starting with
,
we have
The time rate of change of the angular position was called the angular velocity, , for rotation problems in your introductory physics course!!
We now calculate the time
derivative of
by the same procedure.
A graph of the unit vectors and their derivatives may help you visualize the results. It also reminds you that the derivative of a vector produces a vector tangent to the original vector!! The length of the derivative vectors depend on the angular velocity. If there is no rotation then the motion is in a plane and the derivatives of the unit vectors are zero!! If the angular velocity is high then the magnitudes of the derivatives of the unit vectors will be large and these terms will dominate the velocity results.
x y
We are now ready to complete
our relationship for the velocity of an object in Cylindrical
coordinates by substituting in our derivative results and remembering
that
is constant.
Let us now consider our
results. The first term is the radial velocity component. The last
term is the velocity component in the z-direction. If we consider the
special case of a particle traveling in a circle in the x-y plane
then both the first and third terms in the velocity relationship are
zero. Thus, an object moving in a circular path as in your
introductory physics course would have a velocity with a component
only in the
direction
with a magnitude of
.
This is just the tangential velocity from your introductory physics
course!!
In other words, we have
D. Acceleration Vector
We now use the definition of acceleration to develop the relationship for cylindrical coordinates.
Using our relationships for the time derivatives of the unit vectors, we have
Rearranging and combining terms, we have that
The z-component of the acceleration is just due to the change in the z-component of the objects velocity as in the Cartesian coordinate system. However, we see that there are two terms contributing to the acceleration in both the radial and angular directions. The first term in the radial direction occurs if the radial velocity of the object is changing. The first term in the angular acceleration occurs if the object has both angular and radial velocity.
To understand the two
remaining terms, we again consider an object moving in a circle in
the x-y plane. In this case,
and z are constant so
.
Thus, the acceleration becomes
The radial term is the
centripetal acceleration and the angular term is the tangential
acceleration of the object from introductory physics class where
is the angular acceleration.
VI. Transformations Between Coordinate Systems
A. An important use of the
scalar product is to find the component of a vector in the direction
of an arbitrary unit vector. To illustrate this property consider a
vector
.
In Cartesian coordinates, the vector
is
represented as
.
If we take the scalar product of vector
and
the unit vector
,
we get the x-component of vector
as
shown below:
In a similar manner, we can show that
This procedure is not limited
to just the Cartesian coordinate representation. It will work for any
coordinate system whose unit vectors are orthogonal (i.e. the scalar
product of two different unit vectors is zero). For instance if we
represented the vector
using
cylindrical coordinates where
then we have
By a similar procedure, we can also show that
The key thing is not to remember these results, but to understand the process so that you are able to work with any orthogonal coordinate system that you might encounter!!
Let us now use the material
in the previous section to develop relationships for transforming a
vector’s representation in one coordinate system to another.
Let us suppose that we know vector
’s
representation in Cartesian coordinates and want to know its
representation in cylindrical coordinates.
I could simplify these expressions, but I have left them in their most general form so that I can rewrite them in terms of matrices.
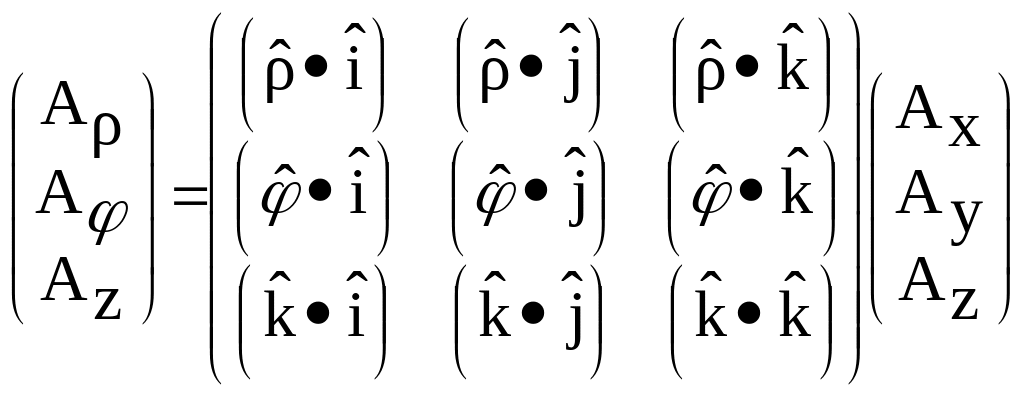
Our result indicates that we can translate between any two orthogonal coordinate systems by multiplying our vector by a transformation matrix whose elements are the scalar product of the unit vectors in these two coordinate systems!!! This process is well suited for computer analysis since computers are extremely efficient at handling matrices (called arrays in CS jargon). In fact, this is the way that rotations and other motion calculations are often handled in video games!!!
Summary:
Find the scalar products between each of the unit vectors
Write the transformation matrix whose elements were found in step 1.
Write your original vector as a column matrix whose elements are the components of the vector in the original coordinate system
Multiply the transformation matrix by the original vector’s column matrix to produce a new column matrix whose elements are the components of the vector in the new coordinate system.
As for our example, we know that
This gives us a transformation matrix of
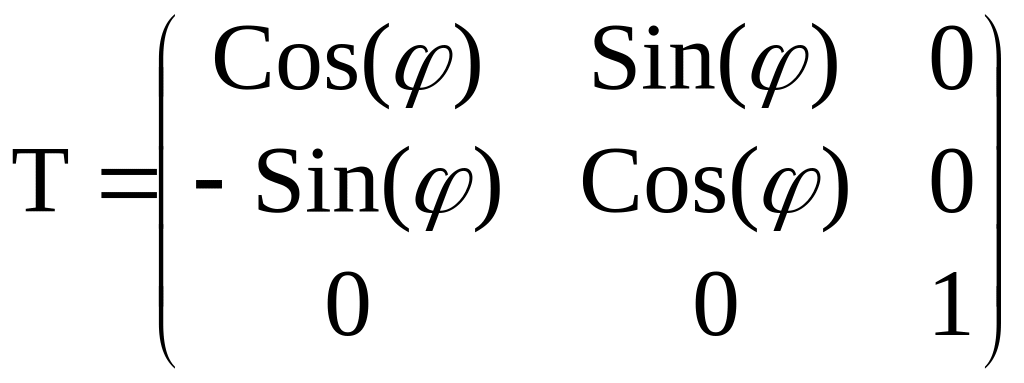
This happens to be the rotation matrix about the z-axis developed in the textbook!!
VII. Other Sources of Information
Schaum’s Outline Series: Math Handbook – Section on Coordinate Systems
Mathematical Methods For Physicists: 5th Ed. By Arfken and Weber : Chapter 1 Sections 1-5, Chapter 2 Sections 1-5, and Chapter 3 Sections 1-3.
VIII. Problems & Questions To Consider
I have left spherical coordinates for you to work out. Some of the question that you might consider if you think that you understand this material are:
What is the determinant of the transformation matrix? What is the
physical significance of this value?
What is the transformation matrix for converting from cylindrical
to spherical coordinates?
What is the transformation matrix for converting from Cartesian
to spherical coordinates?
How do you write the position vector
for a particle in spherical coordinates?
What is the time-derivative of the unit vectors in spherical
coordinates?
How do you write the velocity, and acceleration vectors
for a particle in spherical coordinates?
The scalar product of two vector in Cartesian coordinates is
.
What are the formulas for the scalar product in cylindrical and
spherical coordinates?
1 EDTPA LESSON PLAN PROFESSIONAL GUIDELINES 72314 REVISED 8417
10 AMAZING LIFE LESSONS YOU CAN LEARN FROM ALBERT
10 MICRO I LESSON 3 PREFERENCES LESSON 2
Tags: coordinate systems, on coordinate, lesson, vectors, position, coordinate, systems, vector
- PREGUNTAS Y RESPUESTAS DE UNA ENTREVISTA DE TRABAJO 1
- LA CARTA DEBE IR CON PAPEL MEMBRETEADO DE LA
- PROBLEMAS RESUELTOS CAMPO ELECTRICO 8 CAMPO ELECTRICO I
- BOARD OF REGENTS’ MEETING ACTIVITIES SCHEDULE JUNE 2122 2005
- NEC TECHNOPHILE BUSINESS & EDUCATION SECTORS WITH ITS LCD
- BOARD OF UTAH STATE PARKS AND RECREATION MEETING DEPARTMENT
- DEPARTMENT FOR ENVIRONMENT FOOD AND RURAL AFFAIRS BIODIVERSITY
- LEDARINFORMATION KRISPLAN FÖR LEDARE I EN FÖRENING KAN EN
- CURRICULUM VITAE UNIVERSIDAD DEL CAUCA ADJUNTE UNA FOTOGRAFÍA RECIENTE
- SØKNAD TIL FYLKESMANNEN OM TILSKUDD 2013 FOREBYGGING AV UØNSKEDE
- KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN INSTITUT TEKNOLOGI SUMATERA JALAN TERUSAN
- POWIATOWY ZESPÓŁ SZKÓŁ NR 3 W KOŚCIERZYNIE KOŚCIERZYNA DNIA
- TEMPLATE FOR USE BY BC SOCCER MEMBERS AND AFFILIATED
- TETFUNDESSD10LRPROFILERES BATCH NO OF SUBMISSION………… … TETFUND INSTITUTIONBASED RESEARCH
- T ISKOVÁ ZPRÁVA MANPOWERGROUP INDEX TRHU PRÁCE Q2 2020
- TC ALANYA ALAADDİN KEYKUBAT ÜNİVERSİTESİ LİSANSÜSTÜ EĞİTİM ENSTİTÜSÜ TEZSİZ
- (VARDAS PAVARDĖ) (FAKULTETAS PAREIGOS) KLAIPĖDOS UNIVERSITETO REKTORIUI
- GGI DOWNSCALED SPATIALLY EXPLICIT SOCIOECONOMIC SCENARIO DATA 2007 TECHNICAL
- TEACHING ABOUT SENTENCES SUBJECT KNOWLEDGE FOR TEACHERS’ REFERENCE
- ZAŁĄCZNIK NR 2 DEKLARACJA O REZYGNACJI Z DOKONYWANIA WPŁAT
- MIRÉ LOS MUROS DE LA PATRIA MÍA SI UN
- HEART OF AMERICA COUNCIL TRAILHEAD DISTRICT BOY SCOUTS OF
- CURRICULUM VITAE GYVENIMO APRAŠYMAS VARDAS PAVARDĖ VARDENIS PAVARDENIS
- REPUBLIKA HRVATSKA VUKOVARSKOSRIJEMSKA ŽUPANIJA OPĆINA TOMPOJEVCI OPĆINSKO VIJEĆE KLASA32002150401
- ENTREVISTA CON OSAMA MOHSEN PADRE DE SAID AQUÍ
- ARCHITEKTURA KOMPUTERÓW I PROGRAMOWANIE NISKOPOZIOMOWE 1 HISTORIA EWOLUCJI KOMPUTERÓW
- R OMÂNIA JUDEŢUL TIMIŞ CONSILIUL LOCAL AL ORAŞULUI RECAŞ
- HOW TO USE AN AFFIDAVIT TO GET PERSONAL PROPERTY
- 36 EMPOWERMENT THE INTERSECTION OF IDENTITY AND POWER IN
- PROXECTO LECTOR – ANTROPOLOXÍA HUMANA ¡FELIZ CUMPLEAÑOS LUCY!
CURSO 2017 – 2018 CEIP “LA OLIVARERA” HELLÍNBUSINESS CENTRE CLUB PLAC ŻELAZNEJ BRAMY 10 00136 WARSZAWA
UNSCETDG33INF21 PAGE 2 UNSCETDG33INF21 COMMITTEE OF EXPERTS ONCAPITAL AREA TRANSPORTATION AUTHORITY FREEDOM OF INFORMATION ACT REQUEST
PUBLICADO EL 3 DE FEBRERO DE 1980 EN
EQUILIBRIO DE FUERZAS 1 INTRODUCCION 11CALCULO TEORICO DE UN
OSTRZESZÓW………………………… ZAKŁAD ENERGETYKI CIEPLNEJ SPÓŁKA Z OO UL KĄPIELOWA
YSI 6600 SONDE INSTRUCTION MANUAL VERSION 1 CONTENTS 
U P MÁLAGAMELILLA C CUARTELES 8 29007 MÁLAGA MALAGAUNIDADPROGRESISTAORGTWITTER HTTPTWITTERCOMCURSOESPERANTO 1 SALUTON! LA KURSO DE ESPERANTO EKAS
LA VALIDEZ DE LA FORMACIÓN EN SOCORRISMO ACUÁTICO DR
WHAT TO DO IF A PATRON ALLEGES FOOD POISONING
EXHIBIT LCRRLJ 42(I)(C) IN THE DISTRICT COURT OF THE
PROTOKOLL FORHANDLINGER OM LØNNSREGULERING FOR 2 AVTALEÅR ÅR 2003
HORIZONTE POLÍTICO POR JOSÉ ANTONIO CRESPO ALTERNATIVA ENTRE ALTERNATIVAS
FRANCISCO BERENGUER HISTORIA DE LA COMPUTACIÓN LOS ORÍGENES DE
PROJEKT WSPÓŁFINANSOWANY ZE ŚRODKÓW UNII EUROPEJSKIEJ Z EUROPEJSKIEGO FUNDUSZUCHAPITRE 3 LA MICROECONOMIE ET L’ANALYSE DU FONCTIONNEMENT D’UNE
MICROSOFT WINDOWS SERVER SYSTEM CUSTOMER SOLUTION CASE STUDY BENGALSOUTH TEXAS ELECTRIC COOPERATIVE INCORPORATED SECTION RATES AND CHARGES
